
Чим більше ми розуміємо незнані закони природи,
К.Д.Ушинський, педагог
тим неймовірнішими стають для нас дива.
Яке вміння найважливіше? – Вміння запитувати.
Що таке крива? Відповідь на це просте питання зовсім не така проста, як здається. Виявляється, навіть у рамках елементарної геометрії поняття кривої не має чіткого формулювання. Наприклад, у «Початках» Евкліда вона визначалася як «довжина без ширини», також іноді її визначали як «границю фігури».
Це призвело до того, що фактично в елементарній геометрії вивчення кривих звелося до розгляду окремих прикладів (пряма, відрізок, ламана, коло та ін.). Проте, не маючи загальної теорії і загальних методів, елементарна геометрія досить глибоко проникла у вивчення властивостей конкретних кривих (конічні перерізи, деякі алгебраїчні криві вищих порядків і деякі трансцендентні криві), застосовуючи кожен раз лише спеціальні прийоми.
Досить поширене інтуїтивне або навіть побутове визначення кривої як лінії або сліду, залишеного точкою або тілом, що рухається. При цьому зазвичай криву представляють лише як лінію, що плавно згинається, на зразок параболи або кола. Але математичне поняття кривої охоплює і пряму, і фігури, складені з прямих відрізків, наприклад, трикутник або квадрат. Далі, криві можна поділити на плоскі та просторові. Плоска крива, наприклад парабола, або пряма, утворюється при перетині двох площин або площини і тіла і тому повністю лежить в одній площині.
Просторову ж криву, наприклад гвинтову лінію, що має форму спіральної пружини, не можна отримати як перетин будь-якої поверхні або тіла з площиною, і вона не лежить в одній площині. Зважаючи на складність просторового визначення кривої, надалі матимемо справу лише з плоскими кривими, тобто з тими, що розміщуються на площині. Криві можна також поділити на замкнуті та відкриті. Замкнута крива, наприклад квадрат чи коло, немає кінців, тобто точка, що рухається, породжує таку криву, яка періодично повторює свій шлях.
Формально крива є геометричним місцем, або множиною точок, що задовольняють деякій математичній умові або рівнянню. Наприклад, коло – це геометричне місце точок площини, рівновіддалених від цієї точки. Криві, що визначаються рівняннями алгебри, називаються алгебраїчними кривими. Наприклад, рівняння прямої y = kx + b, де k – кутовий коефіцієнт, а b – відрізок, що відсікається на осі y, – алгебраїчне. Криві, рівняння яких містять трансцендентні функції, наприклад, логарифми або тригонометричні функції, називаються трансцендентними кривими. Наприклад, y = logx та y = tgx – рівняння трансцендентних кривих.
Форму алгебраїчної кривої можна визначити за степенем її рівняння, яка збігається з найвищим степенем членів рівняння. Якщо рівняння першого степеня, наприклад, Ax + By + C = 0, то крива має форму прямої. Якщо рівняння другого степеня, наприклад, Ax2 + By + C = 0 або Ax2 + By2 + C = 0, крива квадратична, тобто є одним з конічних перерізів. Як відомо, конічні перерізи виникають при перетині прямого конуса площиною. Очевидно, що залежно від кута між такою площиною та висотою конуса у перерізі можуть виникати різні фігури. Найбільш відомі загальні форми рівнянь конічних перерізів: x2 + y2 = r2 (коло радіусу r); x2/a2 + y2/b2 = 1 (еліпс); y = ax2 (парабола); x2/a2 – y2/b2 = 1 (гіпербола).
Криві, що відповідають рівнянням третьго, четвертого, п'ятого, шостого тощо степенів, називаються кривими третього, четвертого, п'ятого, шостого тощо порядків. Як правило, чим вищий степінь рівняння, тим більше вигинів буде у відкритої кривої.
Звідки беруться рівняння кривих? Зазвичай це результат детальних математичних досліджень, які, як правило, починаються з визначення умов поведінки кривої. Наприклад, як було сказано вище, коло – це геометричне місце точок площини, рівновіддалених від цієї точки. Якщо таку умову описати математично, то отримаємо відоме компактне рівняння. У багатьох випадках спочатку складається диференціальне рівняння, розв’язком якого є рівняння кривої. Не всі криві вдається описати простими співвідношеннями, чимало їх записуються складнішою параметричною формою, як, наприклад, циклоїда
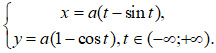
Як бачимо, його не можна записати у вигляді одного співвідношення. А спіраль Корню (або клотоїда, її називають також спіраллю Ейлера) (рис. 1) описується ще складнішою параметричною формою
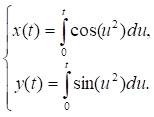
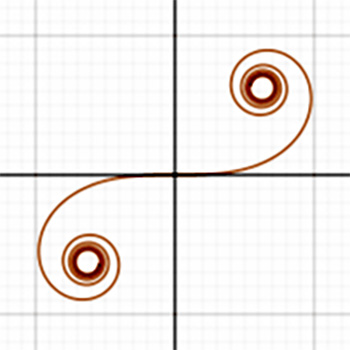
Математики займалися вивченням властивостей кривих з глибокої давнини, і назви багатьох незвичайних кривих пов'язані з іменами тих, хто вперше їх досліджував, наприклад: спіраль Архімеда, локон Аньезі, цисоїда Діоклеса, конхоїда Нікомеда, лемніската Бернуллі, Декартів лист, равлик Паскаля. Деякі назви кривих пов'язані з природною формою предметів або процесів, які вони описують (як, наприклад, ланцюгова лінія, трактриса, строфоїда, кардіоїда, є ціла група спіралей, циклоїд і т.д.).
Як бачимо, кривих величезна кількість і кожна з них має свої унікальні властивості, особливості та сфери застосування. Тут же розглянемо лише одну чудову криву, так звану ланцюгову лінію. Вона має багату, драматичну та навіть майже детективну історію.
Ланцюгова лінія – одна з тих плоских кривих, які ми спостерігаємо повсякденно, можливо, не замислюючись про їх форму – проводи ліній електропередач, мотузки для білизни, ланцюги при вході в музей і т.д. Свою назву ланцюгова лінія отримала через те, що будь-який ланцюжок, закріплений на кінцях, є частиною ланцюгової лінії. Ланцюговою лінією називають криву, форму якої набуває під дією сили тяжіння однорідна гнучка нерозтяжна важка нитка із закріпленими кінцями. З математичної точки зору – це плоска трансцендентна крива. Однак трансцендентною кривою вона стала не відразу.
Яку ж форму приймає ланцюг, що вільно підвішений між двома точками? Великий Галілео Галілей (Galileo Galilei, 1564-1642) вважав, що формою такого ланцюга є парабола. Ось що він писав: «... Інший спосіб накреслити параболу на призмі полягає в наступному. Вб'ємо в стіну два цвяхи на однаковій висоті над горизонтом і на такій відстані один від одного, щоб вога дорівнювала подвійній ширині прямокутника, на якому бажано побудувати параболу; між одним і другим цвяхом підвісимо тонкий ланцюжок, який звисав би вниз і був такої довжини, щоб найнижча точка його знаходилася від рівня цвяха на відстані, що дорівнює висоті прямокутника. Ланцюжок цей, звисаючи, розташується у вигляді параболи, так що, відзначивши її слід на стіні пунктиром, ми отримаємо повну параболу, що розтинається навпіл перпендикуляром, проведеним через середину лінії, що з'єднує обидва цвяхи». Однак, як виявилося пізніше, метр помилявся. Форма ланцюгової лінії відмінна від квадратичної параболи, щоправда, ця відмінність стає помітною лише при достатньому віддаленні від вершини (рис. 2).
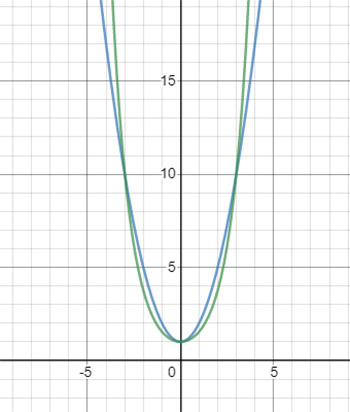
і парабола y = x2 + 1
(парабола знизу вужча, зверху – ширша)
Сумніви у правоті великого Галілея не залишали провідних математиків свого часу майже до кінця XVII століття. Більше півстоліття проблему ланцюгової лінії при її всій простоті і очевидності не вдавалося вирішити, поки в травні 1690 року на сторінках видання (з 1682 по 1782) в Лейпцигу латиною видавцем Отто Менке (Otto Mencke, 1644–1707) щомісячного журналу Acta Eruditorum (Діяння вчених) Якобом Бернуллі (Jakob Bernoulli, 1655-1705) не було опубліковано пропозицію знайти рішення задачі про форму ланцюгової лінії. Якоб Бернуллі був одним з найвидатніших математиків свого часу, проте досі не відомо достовірно, чи вдалося йому самому встановити справжню форму ланцюгової лінії, чи ми повинні дякувати йому лише за своєчасну постановку проблеми. Драматизму ситуації надавала очевидна змагальність математиків за пріоритет своїх результатів і конкуренція старшого (Якоб) і молодшого (Іоганн) братів Бернуллі, що переросла з часом у непримиренність. Як би там не було, через рік, у червні 1691 року три незалежні розв’язки задачі про форму ланцюгової лінії з передмовою видавця були опубліковані в Acta Eruditorum у порядку надходження рукописів до редакції журналу.
Закінчене вирішення питання про форму кривої провисання було досягнуто німецьким математиком Готфрідом Лейбніцем (1646–1716), Християном Гюйгенсом (1629–1695) та швейцарським математиком Йоганном Бернуллі (1667–1748) за допомогою методу нескінченно малих.
Для запису рівняння ланцюгової лінії як осі ординат вибирають вісь симетрії, а вісь абсцис проводять на відстані а від вершини ланцюгової лінії.
Тоді рівняння ланцюгової лінії набуває вигляду

де використана відома математична функція (так званий гіперболичний косинус)
![]() .
.
Відомі також гіперболічні синус, тангенс, котангенс.
Всі ланцюгові лінії подібні одна до одної, зміна параметра а еквівалентна рівномірному розтягуванню або стисканню графіка функції вздовж осі х. Змінна графіка х відраховується від найнижчої точки на осі ординат ланцюгової лінії.
Англійський фізик Роберт Гук (Robert Hooke, 1635–1703) відкрив одну дивовижну властивість ланцюгової лінії: у перевернутому вигляді вона є найстійкішою формою для арок, що стоять окремо. Ланцюг, що провисає, знаходиться в положенні, в якому внутрішні сили розтягують його вздовж лінії кривої, тобто дотичні до ланцюга в кожній її точці. У перевернутому вигляді всі ці сили, що розтягують, перетворюються на сили стиснення, роблячи ланцюгову лінію ідеальною аркою, в якій всі сили стиснення теж діють уздовж лінії кривої. В арці, що має форму ланцюгової лінії, немає згинальних сил: вона підтримує себе власною вагою, не потребуючи, взагалі кажучи, ніяких скоб чи опор. Така арка буде дуже стійкою за мінімальної кількості цегляної кладки. Для того щоб арка стояла міцно, цеглини, в принципі, навіть не потрібно скріплювати цементним розчином, оскільки вони притискають одна одну по всій її висоті. Гук був дуже задоволений своїм відкриттям, заявивши, що «ще жоден архітектор не намагався зробити щось подібне».
Незабаром після цього архітектори та інженери почали використовувати арки – ланцюгові лінії у роботі. До настання комп'ютерної ери найшвидший спосіб створити їх зводився до того, щоб повісити ланцюг потрібної довжини, накреслити криву, побудувати модель із жорсткого матеріалу та поставити її в перевернутому положенні.
Ланцюгові лінії часто зустрічаються в природі та техніці. Так, наприклад, прямокутне вітрило під натиском вітру набуває форми, яка у профілі близька до ланцюгової лінії (це завдання розглядав ще Якоб Бернуллі (1654–1705) – старший брат Йоганна Бернуллі).
Горбатий міст зазвичай проектується у формі, близькій до ланцюгової лінії. Варто, правда, зауважити, що форма вигину тросів підвісного мосту все ж таки ближча до параболи, ніж до ланцюгової лінії. Це пов'язано з тим, що основна вага моста розподілена в полотні мосту, а не в тросах, що підтримують.
На березі річки Міссісіпі в місті Сент-Луїсі стоїть імпозантна арка (Gateway Arch) заввишки 630 футів, що відповідає 192 м, ширина її основи також 192 метри. Таким чином, арка є найвищою пам'яткою на території США. Її будівництво розпочалося 12 лютого 1963 року та було закінчено 28 жовтня 1965 року. Пам'ятник відкрився відвідувачам 24 липня 1967 року (рис.3).
Арка символізує поворотний пункт в американській історії та географії. Сент-Луїс свого часу поєднав відносно обжиті землі на схід від Міссісіпі з дикими безмежними просторами Заходу (рис. 3). Ця арка була спроектована одним із найвідоміших архітекторів США Еро Сааріненом (Eero Saarinen, 1910–1961) у співпраці з математиком та інженером Ганнскарлом Банделем (Hannskarl Bandel, 1925–1993). На арці написано її формулу у футах
y = -127,7’ch(x/127,7’) + 757,7’.
У метрах – це
y = -38,92ch(x/38,92) + 230,95.

В середині арки спроектовано ліфт, а у верхній точці є оглядовий майданчик для відвідувачів.
Видатний іспанський архітектор Антоніо Гауді (Antonio Gaudí, 1982-1926) застосовував досить оригінальний та ефективний спосіб проектування своїх будівель. Вони монтувалися уверх ногами, а уявлення про їх справжній вигляд можна було отримати за допомогою дзеркала. Саме так проектувалася церква Святого Сімейства у Барселоні і саме з використанням ланцюгової лінії!
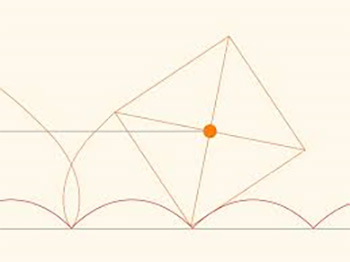
Ось ще одне цікаве застосування ланцюгової лінії. Якщо профіль шосе є перевернуті арки ланцюгової лінії, то ним можна їздити на квадратних колесах, рівно і без трясіння – якщо сторона квадрата колеса дорівнює довжині арки нерівності дороги. Як неважко помітити, тоді центр квадрата увесь час рухається по прямій лінії, тобто на постійній висоті (рис. 4). Якщо простежити за траєкторією руху однієї з вершин квадрата, то виявиться, що вона ніде не перетинається з ланцюговою лінією, а значить, візок, що котиться на квадратних колесах, можна зробити!
У Китаї навіть сконструйовано велосипед на квадратних колесах, на якому може покататися кожний відвідувач.
Ось така дивовижна історія про одну з чудових кривих. Але ж їх багато – увесь світ складається із множини кривих, ми їх бачимо кожен день! Їх треба вивчати і вивчати. Добре відомо, що колись, ще у XIX столітті, в багатьох жіночих школах було навіть запроваджено предмет «Математичне вишивання». На заняттях вивчали спосіб побудови кривих, який називався методом математичного вишивання. Він чудовий тим, що його можна було виконувати кольоровими нитками на шматку тонкого картону. Крім своєї привабливості, вирішення задач способом математичного вишивання дозволяло розширити геометричні уявлення, розвивати акуратність, уважність та працьовитість.
Література:
1. Галилей Г. Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению синьора Галилео Галилея Линчео, философа и первого математика светлейшего великого герцога Тосканского. С приложением о центрах тяжести различных тел. - М.-Л.: Государственное технико-теоретическое издательство, 1934. - С. 273-274.
2. Выгодский М.Я. Справочник по высшей математике. - М.: Наука, Главная редакция физико-математической литературы, 1969. - 872 с.
А.А. Антонюк, кандидат фізико-математичних наук,
Н.Г. Антонюк, кандидат хімічних наук


 Засновник та видавець
Засновник та видавець