Скільки розв’язків (або коренів) має рівняння
|
x2+3x+4=0 ? |
(1) |
Школяр одразу відповість: два, один або жодного, якщо дискримінант виявиться від’ємним. І матиме рацію: квадратні рівняння (точніше, задачу, еквівалентну квадратному рівнянню) навчились розв’язувати ще в 2000 році до нашої ери. Прискіпливий читач відмітить, що насправді розв’язків у квадратного рівняння ЗАВЖДИ два, просто в деяких випадках вони співпадають (кратні корені), а в деяких є комплексними числами, як от у рівняння (1).
Добре, що можна сказати про рівняння
|
x3–7x+6=0 ? |
(2) |
Трійка в степені першого доданку підказує, що воно має три розв’язки. І це правда – в багатьох випадках кубічне рівняння вдається представити у вигляді добутку квадратного рівняння та многочлена першого степеня.
Наприклад, рівняння (2) можна записати так:
|
x3–7x+6=(x–1)(x2+x–6)=0. |
(3) |
Перший множник дає один розв’язок, і ще два отримуємо з квадратного рівняння. Більше того, довільне кубічне рівняння можна звести до рівняння x3+px+q=0 , для розв’язків якого існує аналітична формула, відома під назвою формула Кардано.
Такий же результат маємо для рівняння 4 степеня: воно має 4 корені, для яких існує аналітична формула – так звана формула Феррарі. Досі все складалось чудово. Інтуїція підказує, що для рівняння 5 степеня є рівно 5 розв’язків та гарна аналітична формула для них. Можливо, не така «гарна», як для квадратного чи кубічного рівнянь, але вона має бути. І взагалі, для поліноміального рівняння довільного степеня n має виконуватись два твердження: (а) воно має рівно n коренів та (б) існує «гарна» формула для їх вираження. Чи… ні? Аж ніяк!
Розглянемо твердження (а). За основною теоремою алгебри, довільний відмінний від константи многочлен з однією змінною над полем комплексних чисел має щонайменше один комплексний корінь, звідки неминуче випливає, що многочлен степеня n має n комплексних коренів, враховуючи їхню кратність.
З твердженням (б) ситуація складніша. Для запису розв’язків квадратного, кубічного та рівняння 4 степеня використовуються коефіцієнти цього рівняння, з якими проводять стандартні операції додавання, віднімання, множення, ділення та добування кореня натурального степеня.
Формули цих розв’язків теж ніби «гарні», для рівнянь 3 та 4 степеня трохи об’ємніше ніж для квадратного. Однак після отримання вже згаданих формул Кардано та Феррарі та марних спроб отримати формулу для коренів рівняння 5 степеня, математики замислились: чому отримання цих формул стає дедалі складнішим? Чи існує така формула взагалі? Замислилось багато, а остаточну відповідь дав лише один.

Олівець, портрет з натури
Еварист Галуа (французькою Évariste Galois) народився 25 жовтня 1811 року у Франції, в невеликому містечку Бур-ла-Рен за 9 кілометрів на південь від Парижа. Його батько, Ніколь-Габріел Галуа, був республіканцем та очолював ліберальну партію Бур-ла-Рена. Ймовірно, саме він вплинув на політичні погляди та амбіції молодого Евариста. Його мати, Аделаїда-Марі Галуа, була дочкою юриста, вільно читала латинську та класичну літературу і відповідала за освіту сина протягом перших дванадцяти років його життя.
У жовтні 1823 року молодий Еварист вступив до ліцею Людовика Великого і з 14 років почав серйозно захоплюватись математикою. Вже в 15 років він читав оригінальні статті Жозефа-Луї Лагранжа та Адрієна-Марі Лежандра, призначені для професійних математиків. Примірник «Eléments de Géométrie» Лежандра Еварист прочитав «як роман». Ймовірно, саме роботи цих математиків мотивували Галуа займатись теорією рівнянь у подальшому.
Незважаючи на низьку успішність у школі, Галуа миттєво перестрибнув від елементарної математики до її вищих галузей. У 1829 році вийшла його перша стаття про ланцюгові дроби. У той же час він почав робити фундаментальні відкриття в галузі алгебраїчних рівнянь. Дві його роботи з цієї області після рецензування високо оцінив Огюстен-Луї Коші, видатний математик того часу. Загалом, учителі Галуа відгукувались про нього як про часом незрозумілого у висловленні своїх ідей учня, однак безперечно розумного та вододіючого чудовим дослідницьким духом.
У 1830 році Галуа опублікував три роботи, які в подальшому вплинули на всю математику та її подальший розвиток. Перша робота заклала основи теорії груп та теорії Галуа, яка стосувалась розв’язності поліноміальних рівнянь у радикалах. Друга робота була присвячена чисельному розв’язанню рівнянь, а третя лежала в області теорії чисел, в якій Галуа вперше ввів поняття скінченого поля.
Повернемось до нашого питання: чи існує формула, за якою можна записати розв’язки довільного поліноміального рівняння 5 степеня, використовуючи операції додавання, віднімання, множення, ділення та добування кореня натурального степеня над коефіцієнтами цього рівняння? Іншими словами, чи розв’язне довільне рівняння 5 степеня в радикалах?
Галуа дає чітку та остаточну відповідь на це питання: ні, така формула не існує. Більше того, нерозв’язні також рівняння степенів 6, 7 і вище. Однак варто уточнити, що цей результат не означає, що конкретне задане рівняння 5 чи вище степеня нерозв’язне в радикалах. Зокрема, всі рівняння виду xn–1=0 розв’язні для всіх натуральних n. Розв’язним в радикалах також є рівняння x5+15x+12=0 – нетривіальне рівняння 5 степеня. Однак загальної формули для коренів довільного поліноміального рівняння степеня n при n≥5 не існує. Чому?
Було б неправильним стверджувати, що Галуа придумав і розробив теорію розв’язності поліноміальних рівнянь у радикалах «з нуля». Насправді він скористався здобутками таких відомих математиків як Коші, Лагранж, Руфіні та Абель і просунувся далі. Однією з найбільших заслуг Галуа в розв’язанні цієї проблеми є неочевидний, але вкрай необхідний крок до абстракції. Достатньо було відійти від класичного сприйняття математики як науки про числа та форми і подивитись на неї як на науку про об’єкти, їх властивості та взаємодію – і вона заграла новими фарбами. Одним із проявів такого нестандартного погляду Галуа було введення в математику нового об’єкта – групи.
Що таке група? Формально, це множина об’єктів (називаються елементами), для яких введено певну операцію взаємодії між собою, що задовольняє декілька природних властивостей. Наприклад, у групі завжди існує об’єкт, який при взаємодії з іншим об’єктом ніяк його не змінює – такий елемент називається одиничним. Зокрема, в множині натуральних чисел таким елементом є одиниця: помноживши будь-яке натуральне число на неї, ми знову отримаємо це число.
У груп є низка різних цікавих властивостей, однак загалом це досить «сухі» математичні об’єкти. По-справжньому групи розкриваються тоді, коли виникають як множини всіх перетворень (симетрій) певної структури. Іншими словами, елементами групи є такі перетворення структури, які не змінюють її.
Для прикладу, розглянемо звичайний рівносторонній трикутник на площині. Всього є шість перетворень, які не змінюють цей трикутник: три повороти відносно осей, що проходять через середину кожної сторони та протилежну вершину (L1, L2 та L) , а також три повороти відносно центра трикутника за годинниковою стрілкою на 120, 240 та 360 градусів (R120, R240 та I). Поворот на 360 градусів переводить трикутник у вихідне положення, тому зазвичай позначається I=id (від англійського слова identity – тотожність).
Пронумерувавши вершини трикутника цифрами від 1 до 3 у певному порядку, можна геометрично зобразити всі шість перетворень (рис. 1). Кожному трикутнику відповідає набір з трьох чисел, який однозначно його ідентифікує. Наприклад, трикутнику I відповідає трійка (1,2,3), а трикутнику, отриманому в результаті перетворення L2 – (2,1,3).
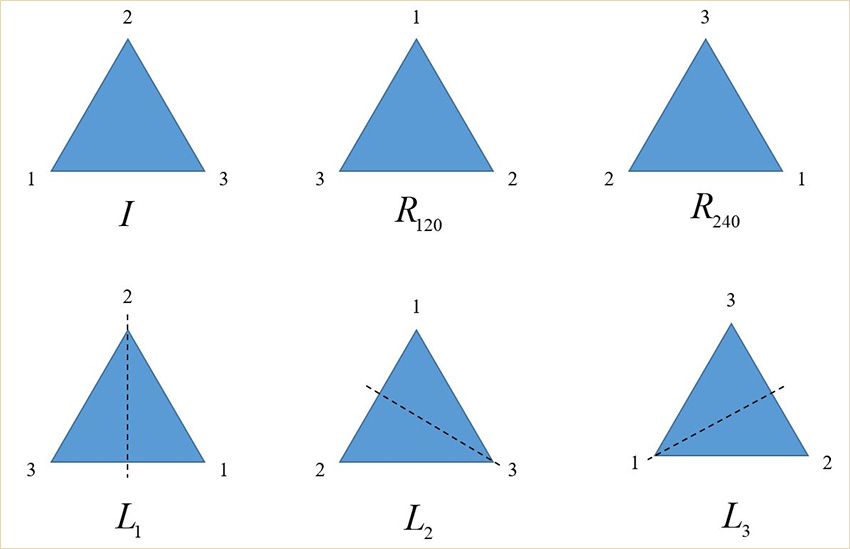
Ці шість перетворень і утворюють групу тотожних перетворень рівностороннього трикутника: I, R120, R240, L1, L2, L3. Така група називається діедральною і позначається D6, де індекс вказує на кількість елементів групи.
Згадуємо, що в групі має бути введена операція взаємодії між її елементами – тут це послідовне виконання двох перетворень. Наприклад, вираз L1∙R120 означає, що ми маємо спочатку повернути наш трикутник на 120 градусів за годинниковою стрілкою, а потім відобразити його відносно вертикальної осі. Неважко помітити, що в результаті ми отримаємо трикутник (2,1,3). Зверніть увагу: результатом перетворення L1∙R120 є трикутник (2,1,3), який співпадає з трикутником, який ми отримуємо в результаті операції L2!
Це і є одна з найважливіших властивостей групи, яку помітив Галуа: результатом дії операції групи над двома елементами завжди є елемент цієї ж групи. Тобто, має місце рівність L1·R120=L2. Якщо кількість елементів у групі є невеликою, можна записати «табличку множення»: результати дій операції групи між кожними двома елементами. Такі таблиці називаються таблицями Келі на честь англійського математика Артура Келі, що жив у ХІХ столітті.
Група симетрій трикутника є зручною для геометричного представлення, однак її можна також розглядати як групу перестановок на трьох елементах. Оскільки кожен трикутник на рисунку 1 однозначно задається впорядкованою трійкою чисел, ми можемо розглянути групу таких трійок – це і буде група перестановок на трьох елементах. Така група називається симетричною і позначається S3. Більше того, група S3 є ізоморфною до діедральної групи D6, тобто ці дві групи та їх властивості повністю співпадають, хоч і називаються по-різному.
Добре, є група симетрій трикутника, група перестановок, але… до чого тут поліноміальні рівняння? Дуже просто: корені такого рівняння можна записати у вигляді впорядкованого списку, тобто перестановки. Певні дуже фундаментальні властивості рівнянь пов’язані зі зміною порядку в такому списку. Зокрема коефіцієнти рівняння мають бути симетричними виразами від коренів, тобто виразами, які не змінюються, якщо корені цього рівняння міняють місцями. Так і проявляється та симетрія, яку ми зустрічали, розглядаючи групу перетворень трикутника.
Саме групами перестановок коренів поліноміальних рівнянь і займався Галуа. Для кожного рівняння такого виду можна виписати групу перестановок коренів цього рівняння. Після чого можна дослідити симетрії цього рівняння, тобто такі перестановки, які зберігають всі співвідношення між його коренями.
Наприклад, ми маємо два корені певного рівняння х1 та х2, для яких виконується співвідношення х1 - х2 = 4. Розглянемо перестановку (2,1,3), яка третій корінь лишає незмінним, а перші два міняє місцями. Це означає, що також має виконуватись рівність x22–x1=4. Якщо не виконується – перестановка (2,1,3) не є симетрією. Інакше ми продовжуємо перевіряти аналогічним чином всі інші можливі алгебраїчні співвідношення між коренями, і якщо вони всі виконуються – перестановка (2,1,3) є симетрією.
Звучить занадто складно? Можливо, однак є одне твердження, що робить обчислення симетрій доцільним: група всіх симетрій довільного рівняння має бути підгрупою в групі перестановок його коренів. Підгрупа – одне з фундаментальних понять теорії груп, яке означає, що певна підмножина елементів групи з груповою операцією сама поводить себе як повноцінна група. Тому в дослідженні групи симетрій певного рівняння та її зв’язку з групою перестановок коренів лежить вся таємниця розв’язності рівнянь у радикалах.
Група симетрій заданого рівняння отримала назву групи Галуа на честь свого творця і що б вона собою не являла – в ній лежить вся необхідна інформація про корені цього рівняння. Для перевірки його розв’язності Галуа створив певний процес, який полягає в побудові послідовності вкладених одної в одну підгруп. Першою групою в цій послідовності є група Галуа заданого рівняння, останньою підгрупою має бути тривіальна група. Кожна підгрупа в цій послідовності має бути групою спеціального виду, яка називається нормальною.
Якщо для заданого рівняння вдається побудувати таку послідовність вкладених підгруп – воно розв’язне в радикалах, інакше – ні. Звучить просто, але не дуже зрозуміло. Тому давайте розглянемо цей процес на прикладі загального рівняння 5 степеня. Таке рівняння має 5 коренів, для яких існує 120 перестановок (5!=120). Оскільки коефіцієнти рівняння є повністю симетричними, його група Галуа містить всі 120 перестановок – ця група є першою в послідовності.
Як і навіщо здійснюється пошук нормальних підгруп? Справа в тому, що симетрії рівняння змінюються, коли у формулі кореня рівняння з’являються радикали, тобто операції добування кореня натурального ступеня. Галуа показав, що при взятті кореня степеня p група Галуа має розбиватись на p різних блоків однакового розміру (Абель, до речі, довів, що число p завжди можна брати простим, що значно спрощує процедуру). Причому один з утворених блоків має бути нормальною підгрупою індексу p.
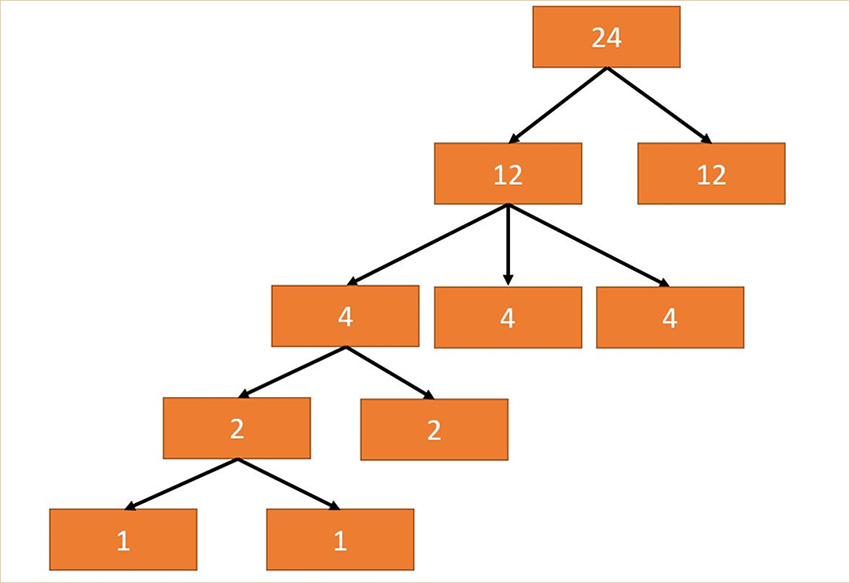
Отже, починаємо процес з групи Галуа рівняння 5 степеня. Ця група містить 120 елементів, тому нормальна підгрупа в ній може бути індексу 2, 3 або 5 – це прості дільники числа 120 (згадуємо Абеля). Ці індекси відповідають операціям добування кореня степеня 2, 3 або 5 у формулі кореня рівняння. Нехай формула починається з добування кореня 5 степеня, отже, група Галуа ділиться на 5 блоків по 24 елементи в кожному – це відповідає нормальній підгрупі індексу 5. Але Галуа простими операціями з перестановками зміг довести, що такої підгрупи в цій групі Галуа не існує. Отже, п’ятірка «відпадає». Беремо трійку: три групи по 40 елементів. На жаль, тут нас теж спіткає невдача: нормальної підгрупи індексу 3 в нашій групі Галуа не існує. Лишається останній варіант: шукати нормальну підгрупу індексу 2 – і така є! Причому рівно одна. Ця група містить 60 перестановок і називається знакозмінною. Наявність цієї групи та відсутність інших означає, що будь-яка формула для кореня рівняння 5 степеня має починатись з операції взяття квадратного кореня.
Продовжуємо процес далі: в знакозмінній підгрупі з 60 перестановок шукаємо нормальну підгрупу індексів 2, 3 і 5, оскільки прості дільники числа 60 саме такі. Однак, працюючи з тими ж перестановками з 5 елементів, Галуа показав, що знакозмінна підгрупа взагалі не містить нормальних підгруп. Це означає, що наш процес закінчується неуспіхом – ми не змогли побудувати послідовність підгруп, починаючи з групи Галуа рівняння 5 степеня, остання з яких – тривіальна підгрупа. Це означає не що інше, як те, що рівняння 5 степеня є нерозв’язним в радикалах. Більше того, рівняння 6, 7 і вище степеня теж є нерозв’язними в радикалах, і це можна показати, скориставшись аналогічним підходом. Отже, якісний погляд на корені рівняння дозволяє отримати інформацію про розв’язність самого поліноміального рівняння, причому довільного степеня.
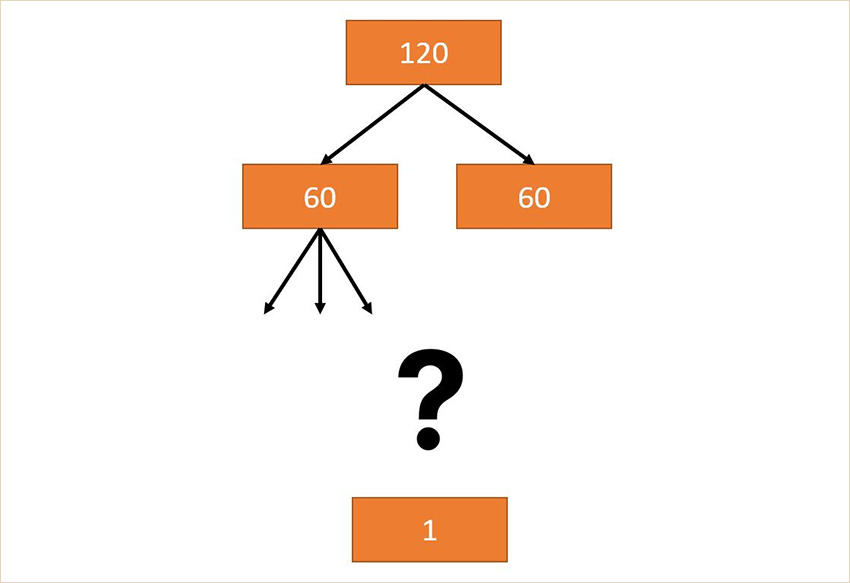
Щоб краще зрозуміти описаний процес, його можна продемонструвати геометрично як процес побудови певного дерева, коренем якого є група Галуа, листям – тривіальні групи. Мета процесу – з’єднати корінь та всі листки дерева. При знаходженні нормальної підгрупи індексу p з кореня виходять p нових віток. Одна з цих віток відповідає нормальній підгрупі індексу p, в якій буде здійснюватися пошук нової нормальної підгрупи. Процес продовжується, доки вітки не з’єднаються з усіма листками, або буде показано, що таке з’єднання неможливе. Графічне зображення побудови такого дерева для рівняння 5 степеня наведено на рисунку 2.
Повернемось до розв’язних рівнянь, якими є рівняння 4, 3 та 2 степеня (очевидно, лінійне рівняння 1 степеня теж розв’язне). Теорія Галуа має пояснювати, чому вони є розв’язними, тобто має існувати відповідна послідовність нормальних підгруп з відповідними індексами. Так, вона існує. Наприклад, графічне зображення, чому рівняння 4 степеня розв’язне, наведено на рисунку 3. Ця схема не лише доводить розв’язність рівняння, а й дозволяє побачити, який вигляд матимуть його корені. А звідси вже недалеко до виписування самих коренів.

Загалом, результати Галуа без перебільшення призвели до революції в теорії рівнянь, оскільки його теорія дозволяє зазирнути в саму суть рівняння і дізнатись про нього практично все. Ну, майже все.
Задача, яку ставив перед собою Галуа, була прозорою та зрозумілою, але водночас суто теоретичною. Це призводить до важливого недоліку цієї теорії: вона неспроможна відповісти на питання чи розв’язне конкретне задане поліноміальне рівняння. Очевидно, всі рівняння до 4 степеня включно точно розв’язні. Раніше ми вказували, що рівняння xn–1=0 розв’язне для довільного натурального n. Як щодо рівняння x5–6x+3? Невідомо. Максимум, який можна зробити, це виписати групу Галуа цього рівняння і дослідити її.
Проблема теорії Галуа полягає в тому, що вона працює з коренями, а не коефіцієнтами рівняння, і, фактично, відповідає на питання, які властивості цих коренів роблять рівняння розв’язним чи нерозв’язним. До речі, вищенаведене рівняння нерозв’язне в радикалах.
Навряд чи Галуа знав, який вплив його роботи здійснять на подальший розвиток математики. В математиці часто буває так, що конкретний учений береться за складну задачу, яку століттями безуспішно намагались розв’язати інші, і… не розв’язує її. Однак в процесі роботи над нею, він створює набір новітніх і часом революційних методів, які або суттєво приближують розв’язання поставленої задачі, або знаходять своє застосування в зовсім іншій області математики або науки загалом. Так сталось і з Галуа. Станом на сьогодні теорія груп є однією з найважливіших розділів сучасної математики та алгебри. Її елементи виникають у майже всіх областях математики, а сама теорія знаходить свої численні застосування в хімії, біології, квантовій фізиці, кристалографії та багатьох інших розділах науки.
За своє життя він регулярно брав участь у виступах республіканців, вів себе зухвало та неодноразово потрапляв до в’язниці. 31 травня 1832 року Еварист Галуа загинув на дуелі. Справжні мотиви дуелі невідомі. Певні джерела стверджують, що ця дуель мала під собою політичні мотиви.
Галуа прожив лише 20 років, з яких всього 4 роки він займався математикою. Можна тільки здогадуватись, яких успіхів він би досягнув, якби прожив довше. Однак його досягнення та внесок у розвиток тогочасної математики ставлять Галуа на один рівень з найкращими математиками XIX століття.
Віктор Стовба, доктор філософії (PhD), молодший науковий співробітник Інституту кібернетики імені В.М. Глушкова НАНУ


 Засновник та видавець
Засновник та видавець