…Каждый из студентов, постигавших премудрости одной из многих технических специальностей в аудиториях и лабораториях институтов и техникумов прошлого столетия провёл не одну бессонную ночь над бесконечной вереницей чертежей, выполненными ими на листах ватмана, прикрепляемых кнопками к чертёжной доске кульмана.
Нередко такие студенты непростые пять или пять с половиной лет учёбы в институте делили на своеобразные этапы: сдал «начерталку» (т.е. начертательную геометрию на первом курсе) – можно влюбиться, а сдал «сопромат» (сопротивление материалов на втором курсе) – можно жениться!
Также аббревиатуру одной из учебных дисциплин третьего курса – ТММ (теория механизмов и машин) иначе как «Ты Моя Могила» никто и не расшифровывал. После этого следовали «детали машин» с их редукторами и ременными передачами, «подъёмно-транспортные машины», а уж затем, наконец, и многочисленные специальные дисциплины. И все они предполагали выполнение студентом чертежей на ватмане формата А1 (597×841 мм – ровно половину квадратного метра).
В большинстве случаев чертежи выполнялись с помощью кульмана – изобретённого немецким инженером Францем Кульманом (1877–1965) чертёжного прибора в виде доски, установленной вертикально или под некоторым углом к вертикали. (К своему стыду, автор этих строк так и не привык к работе на этом инструменте, т.к. в двухкомнатной киевской «хрущёвке», где проживали пять человек, ему просто не было места, а все чертежи выполнялись на кухонном столе в перерывах между приёмами пищи членами многочисленной семьи).

Кульман – достаточно точное устройство, обеспечивающее возможность проведения прямых линий заданной длины под любым углом в плоскости чертёжной доски. Это прибор пантографного типа, состоящий из системы рычагов, соединённых шарнирно в виде параллелограмма, либо координатного типа, имеющий два взаимно перпендикулярных профиля, по которым перемещаются каретки.
Система параллелограммов и одна из кареток снабжены делительной (угломерной) головкой с двумя взаимно перпендикулярными масштабными линейками. Линейки могут иметь различный масштаб и различную длину – горизонтальная обычно 500 мм, а вертикальная – 300 мм. Линейки изготовляют из усиленной металлом пластмассы или из тонкостенного стального профиля.
Угломерная головка прибора обеспечивает высокую точность отсчёта угла (с фиксацией угла поворота головки обычно через 15° и реже – в произвольном положении) и имеет две шкалы отсчёта (прямую и обратную), а также приспособление для их смещения, чтобы выполнять построение проекций под необходимым углом.
Кульман также мог снабжаться тормозами для фиксации положения головки и чертёжной доски, приспособлениями для юстировки линеек, приспособлениями для выполнения штриховки и некоторыми другими.
Разработка чертежей с помощью кульмана велась в отдельных плоскостях: вид спереди, вид сбоку, вид сверху. Иными словами, с его помощью реализовывалось, как сегодня принято выражаться, 2D конструирование (т.е. двумерное конструирование).

Современные же компьютерные технологии позволяют проектировать сразу в трёх измерениях (3D конструирование), в том числе, применяя обратный подход, т.е. переход от трёхмерной модели к чертежам для отдельного вида, разреза или сечения на плоскости.
Однако, прежде чем с помощью кульмана приступить к выполнению чертежа, в большинстве случаев нужно было предварительно рассчитать проектируемые деталь или сборочную единицу. И обойтись здесь таблицей умножения и выполнением в столбик простейших арифметических операций никак не удавалось. Требовалась помощь более серьёзного вычислительного инструментария, неизменными представителями которого многие десятилетия являлись таблицы Брадиса и логарифмическая линейка.
...В школьные и студенческие годы, пользуясь незаменимыми тогда таблицами Брадиса, я и не подозревал, что их автор – Владимир Модестович Брадис (1890–1975) – вовсе не иностранец, как считали некоторые, а вполне «наш человек», советский математик-педагог, заслуженный деятель науки РСФСР, доктор педагогических наук, профессор, почти четыре десятилетия (с 1920 по 1959 гг.) проработавший в Тверском институте народного образования, а затем Калининском педагогическом институте (ныне Тверской государственный университет).
Сегодня для того чтобы узнать, чему равен, например, sin(25°) либо cos(25°) нужно воспользоваться калькулятором либо соответствующим приложением своего мобильного телефона и получить нужный ответ «0,4226» либо «0,9064».
Калькулятор выдаёт эти значения (при этом точность искомой величины обычно намного выше), пользуясь давно известным математикам способом разложения функций в виде степенных рядов. Так, функцию sin(x) можно записать в виде следующего ряда:
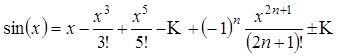
а функцию cos(x), соответственно:
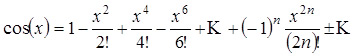
Использование подобных формул позволяет определить значение функции практически с любой точностью, поскольку соответствующие формулы содержатся в памяти калькулятора.
На практике же, большая точность обычно не нужна, а, оказывается, достаточно трёх или четырёх значащих цифр (в данном случае цифр после запятой). Заслуга же Брадиса заключается в том, что он обосновал способ, позволяющий до минимума сократить утомительные вычисления.
Для этого математик отобрал наиболее распространённые для инженерных расчётов функции, определил их значения с достаточной для инженерных расчётов точностью в необходимом интервале аргументов и представил в виде удобных для пользования таблиц.
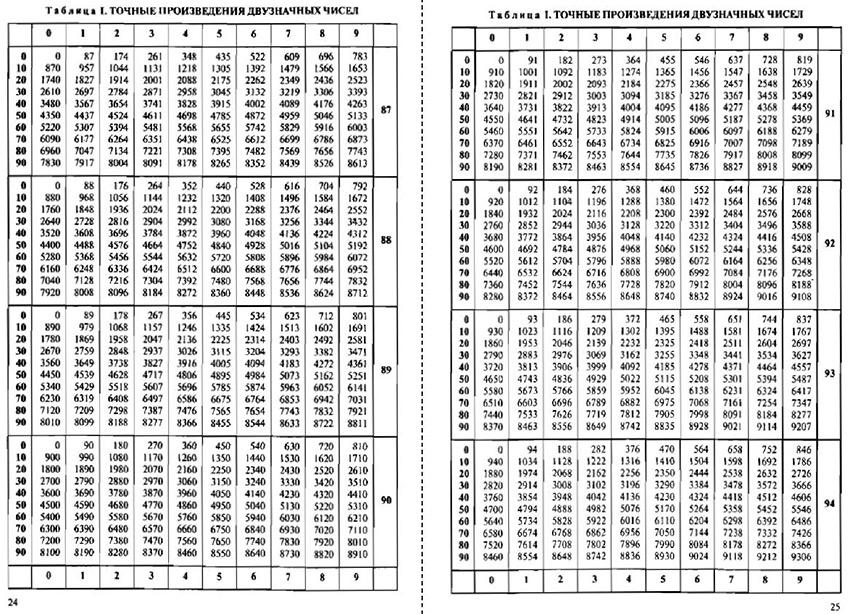
Потрудиться Владимиру Модестовичу пришлось изрядно, однако его труд оказался как нельзя кстати для школьников и студентов, инженеров и учёных. Проведенные им расчёты экономили драгоценное время не одному поколению расчётчиков.
Впервые изданные в 1921 году «Таблицы четырёхзначных логарифмов и натуральных тригонометрических величин», которые позднее издававшиеся под названием «Четырёхзначные математические таблицы», вплоть до конца 1970-х годов переиздавались почти ежегодно. Редкая книга может поспорить с таблицами Брадиса в массовости.
Так, 13-е стереотипное издание упомянутых таблиц, напечатанное московским издательством «Дрофа» в 2010 году, кроме двадцати двух таблиц содержит также главы «Объяснения к таблицам» и «Важнейшие формулы по курсу математики для 7 и 8 классов». А сами таблицы содержат следующую полезную информацию:
Таблица I. Точные произведения двухзначных чисел.
Таблица II. Значения дробей вида 1/n.
Таблица III. Квадраты.
Таблица IV. Квадратные корни.
Таблица V. Кубы.
Таблица VI. Длина окружности диаметра d.
Таблица VII. Площадь круга диаметра d.
Таблица VIII. Синусы и косинусы.
Таблица IX. Тангенсы и котангенсы.
Таблица X. Тангенсы углов, близких к 90°, и котангенсы малых углов.
Таблица XI. Радианная мера.
Таблица XII. Тригонометрические функции от аргумента в радианах.
Таблица XIII. Мантиссы десятичных логарифмов.
Таблица XIV. Значения функций 10x (десятичные антилогарифмы).
Таблица XV. Логарифмы синусов малых углов и косинусов углов, близких к 90°.
Таблица XVI. Логарифмы синусов углов от 14 до 90° и косинусов углов от 0 до 76°.
Таблица XVII. Логарифмы тангенсов малых углов и котангенсов углов, близких к 90°.
Таблица XVIII. Логарифмы тангенсов и котангенсов углов от 14 до 76°.
Таблица XIX. Логарифмы тангенсов углов, близких к 90°, и котангенсов (дополнительных) малых углов.
Таблица XX. Разные таблицы (натуральные логарифмы, приближённые формулы, биномиальные коэффициенты).
Таблица XXI. Номограмма для решения уравнения 1/x+1/y+1/z.
Таблица XXII. Номограмма для решения уравнения z2+pz+q=0.
Кроме упомянутых таблиц, которые постоянно носить с собой было не совсем удобно, другое счётное приспособление – логарифмическая линейка – легко размещалась в кармане пиджака студента или белого халата конструктора. Этот удивительный деревянный или пластмассовый «брусок» позволял быстро перемножать и делить любые числа и извлекать квадратные и кубические корни, возводить в степень, вычислять тригонометрические и логарифмические функции. Этот инструмент существенно облегчал расчёты человеку не только на Земле, но и в Космосе.
...От утомительных расчётов в столбик в начале XVII века всех спас шотландский математик Джон Непер (1550–1617), о котором немецкий математик, астроном, механик и оптик, первооткрыватель законов движения планет Солнечной системы Иоганн Кеплер (1571–1630), потративший годы на сложные астрономические вычисления, отозвался так: «Некий шотландский барон, имени которого я не запомнил, выступил с блестящим достижением: он каждую задачу на умножение и деление превращает в чистое сложение и вычитание».
Прекрасно понимая, какой мощный инструмент он подарил человечеству, Непер писал в предисловии написанного им в 1614 году «Каноне о логарифмах»: «Осознав, что в математике нет ничего более скучного и утомительного, чем умножение, деление, извлечение квадратных и кубических корней, и что названные операции являются бесполезной тратой времени и неиссякаемым источником неуловимых ошибок, я решил найти простое и надежное средство, чтобы избавиться от них».
В изданной Непером в 1614 году работе «Описание удивительной таблицы логарифмов» он изложил свойства логарифмов, дал описание таблиц, а также правила пользования ими и примеры применений.
Основанием таблицы логарифмов Непера является иррациональное число, к которому неограниченно приближаются значение выражения вида (1+1/n)n при неограниченном возрастании n. Это число называют «неперовым числом» и обозначают буквой е:
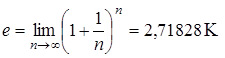
Получается, что логарифмы – головная боль старшеклассников – были придуманы для того, чтобы в дальнейшем облегчить им жизнь.
Непер не без оснований полагал, что это именно так: «Отбросьте числа, произведение, частное или корень которых необходимо найти, и возьмите вместо них такие, которые дадут тот же результат после сложения, вычитания и деления на два и на три».
Иными словами, используя логарифмы, умножение удалось упростить до сложения, деление превратить в вычитание, возведение в квадрат и третью степень, а также извлечение квадратного и кубического корней – в умножение и деление на два и на три, соответственно:
lg(xy) = lg(x) + lg(y) и lg(x/y) = lg(x) – lg(y);
lg(x2) = 2lg(x) и 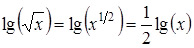 .
.
Т.е. для того, чтобы перемножить два произвольных числа, с помощью таблицы логарифмов нужно определить и сложить их логарифмы, после чего найти в таблице число, логарифм которого равен полученной сумме, и определить почти точное значение искомого произведения.
Используя логарифмы, Иоганн Кеплер в начале XVII века рассчитал орбиту Марса, а потом и других планет, выведя, в конце концов, законы движения небесных тел по своим орбитам.

(вверху указаны значения
логарифмов нижних чисел)
Однако на практике находка Непера оказалась не очень удобной, поскольку для проведения расчётов было необходимо всегда иметь под рукой таблицы логарифмов. И тогда в 1620 году лондонский математик Эдмунд Гюнтер нанес на линейку шкалу, на которой положение каждого числа было пропорционально его логарифму. После этого для перемножения двух чисел стало достаточным зафиксировать циркулем расстояние от начала шкалы до первого сомножителя, затем установить одну его ножку на втором сомножителе и прочитать число, на которое укажет другая ножка. Работать стало несколько проще. Но… иметь дело с циркулем с острыми ножками всё же было не совсем удобно.
И вот в 1622 году англиканский священник Уильям Отред (1575–1660), выпускник Итонской школы и Кембриджского королевского колледжа, отказался и от циркуля. Он расположил рядом две подвижные логарифмические шкалы и создал первую в мире логарифмическую линейку. Позднее он изготовил и её круговой аналог.
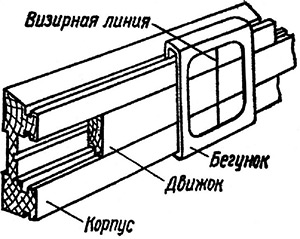
линейки с движком
Логарифмическая линейка состоит из корпуса (линейки), движка и бегунка; на бегунке имеется визирная линия.
На кор¬пусе и движке нанесены числовые шкалы. Шкалы A и B называются основными; с помощью этих шкал производится большинство вычислений, которые можно выполнять на линейке.
В частности, шкалы A и B предназначены для выполнения действий умножения и деления чисел, а также для ре¬шения пропорций.
Шкалой L пользуются для нахождения логарифмов чисел. По шкале C определяются квадраты, а по шкале K – кубы чисел.
Применяя обе шкалы вместе, можно находить и другие натуральные степени чисел. Кроме того, с помощью шкал C и K извлекаются квадратные и кубические корни из чисел.
Шкала R предназначена для нахождения чисел, обратных данным. На оборотной стороне движка имеются шкалы S (от Sin), Т (от Tg) и S & Т, которые называются тригонометрическими и служат для нахождения значений тригонометрических и обратных тригонометрических функ¬ций.
Все шкалы логарифмической линейки, кроме шкалы L, имеют неравномерные деления и называются логарифмическими, а шкала L имеет равномерные деления. Так как шкалы линейки (за исключением шкалы L) – логарифмические, то и линейку называют логарифмической.
Шкалы A и B, а также C и D – попарно одинаковые. Против каждого: числа x на шкале B находится его десятичный логарифм y=lg(x) на шкале L, а против каждого числа y на шкале L находится число x=10 y на шкале B.
Чтобы найти произведение x0=x1x2 двух чисел x1 и x2, устанавливают движок так, чтобы левая единица шкалы A совместилась с отметкой числа x1 на шкале B. Против отметки числа x2 шкалы A на шкале B находим произведение x0=x1x2. На шкале L против отметки числа x1 шкалы B находится число y1=lgx1, против отметки числа x2 шкалы A (с выдвинутым движком) – число y=lgx1+lgx2; поэтому на шкале B против числа y=lgx1+lgx2 шкалы L находится число x0=x1x2.
Аналогично объясняется принцип выполнения на логарифмической линейке действия деления чисел.

линейки с движком
Отред не придавал особого значения своим изобретениям, а своих многочисленных учеников учил совершенно бесплатно. Этими качествами характера Отреда воспользовался в 1630 году один из его учеников. Ричард Деламейн напечатал статью о круговой логарифмической линейке, в которой объявил себя автором изобретения. Тут уж Отред разгневался и обрушился на Деламейна, упрекая того в заимствовании чужой идеи. Скандал длился много лет и затих лишь после смерти Деламейна.

линейка «Спутник»
Так или иначе, с появлением линейки Отреда логарифмические таблицы стали практически не нужными: чтобы перемножить два числа, достаточно было просто совместить цифры на шкалах и прочитать ответ. И всё же, несмотря на портативность и удобство, логарифмическая линейка получила всеобщее признание только спустя два столетия.
В 1850 году английский математик Август де Морган всё ещё удивлялся консервативности своих коллег: «Многие до сих пор жалеют несколько шиллингов на приобретение карманного устройства, облегчающего сложнейшие вычисления в сотни раз!»
В первой половине XIX века логарифмическая линейка была усовершенствована. В 1814 году Питер Роджет представил Королевскому научному обществу линейку с двойной логарифмической шкалой, которая позволяла без труда вычислять дробные степени и корни.
Широкую известность логарифмической линейке принес 19-летний французский артиллерист Амадей Манхейм. В 1850 году он выбрал четыре самые полезные шкалы и добавил бегунок (подвижный указатель, помогающий совмещать числовые отметки).
В 1921 году лондонский инженер Отис Кинг вспомнил об опыте Отреда, свернул полутораметровую логарифмическую шкалу в спираль и нанес её на поверхность стержня диаметром в один дюйм (25,4 мм). Устройство обеспечивало точность до четырех знаков. Ещё на порядок точнее была линейка Фуллера: представлявшая собой цилиндр высотой 30 см с навитой на него 12-метровой шкалой.
Во время Второй мировой войны для военно-воздушных сил США была изобретена особая логарифмическая линейка: в алюминиевый корпус с пластиковым бегунком вставлялись специализированные целлулоидные шкалы для расчета высоты, дальности полёта и расхода горючего (целлулоид – пластмасс на основе нитрата целлюлозы; используется, например, для изготовления шариков для настольного тенниса).
Были и другие усовершенствования этого полезного изобретения.
Линейки, выпускавшиеся в СССР, в отличие от линейки на фото, почти всегда имели дополнительную сантиметровую шкалу у скошенного края, как и у обычной линейки. Стандартная линейка имела длину 30 см, что было удобно для геометрических работ с форматом A4. При этом логарифмические шкалы имели длину 25 см, на концах обычно наносились их обозначения. Реже встречались линейки малого размера со шкалами вдвое короче – длиной 12,5 см и вдвое большого размера – со шкалами длиной 50 см.
…Сегодня некогда популярные кульман, таблицы Брадиса и логарифмическая линейка практически не используются: их заменили быстрые и надёжные компьютеры и калькуляторы.
Тем не менее, они достойны уважения: ведь именно с их помощью были выполнены чертежи и рассчитаны многочисленные технические разработки прошлого, многими из которых мы пользуемся и поныне!
Источники информации
1. Линейка для Луны // Юный техник. – 2011. – № 10.
2. Марк Блау. Чем прославился В.М. Брадис? Конечно, таблицами Брадиса!.
3. Логарифмическая линейка: Всё о Hi-Tech.
И.О. Микулёнок, доктор технических наук, профессор, КПИ им. Игоря Сикорского










 Основатель и издатель
Основатель и издатель Copyright © 2016–2021 Научно-популярный
Copyright © 2016–2021 Научно-популярный