Настоящие заметки о приближенных вычислениях автор адресует в первую очередь тем, кто интересуется точными науками. Понятно, что те, кому это неинтересно, всегда с полным основанием воспользуются калькулятором, и тут даже не нужно уметь делить или умножать, не говоря о более сложных операциях. Здесь мы не станем убеждать возможных оппонентов о пользе или бесполезности тех приёмов, которые будут описаны ниже.

А теперь, когда остались заинтересованные слушатели, поставим первый вопрос.

Нельзя ли с помощью простого калькулятора с операциями +, –, ×, :, 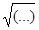 извлечь корень кубический или другой степени, не кратной двум?

Оказывается, такая возможность есть. Ниже для наглядности вместо знака корня будем использовать степенную запись, то есть, вместо 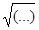 пишем (…)^1/2.

Рассмотрим уравнение:

y^1/2 = x^1/3.

Заметим, что число под корнем всегда можно привести к конечному целому числу, например, (5,387)^1/5 = 0,1·(5,387·10⁵)^1/5 = 0,1·(538700)^1/5. Также очевидно, что всегда y < x.

Можно выразить у через произведение величин x в степенях вида (½)ⁿ.

В самом деле, имеем

x = y^3/2 = y·y^1/2,

отсюда, многократно вставляя вместо y его значение в виде x/y^1/2, получим

y = x/y^1/2 = x/(x/y^1/2)^1/2 = x^1–1/2y^1/4 = x^1–1/2(x/y^1/2)^1/4 = x^{1 – 1/2 + 1/4} y^–1/8 =

= x^{1 – 1/2 + 1/4} (x/y^1/2)^–1/8 = x^{1 – 1/2 + 1/4–1/8} y^–1/16 и т.д.

Поскольку y < x ≤ а, где а – конечное число, при (1/2)ⁿ → 0 будем иметь 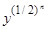→1.

Полученное произведение дает представление числа y^1/2, а значит и искомого x^1/3 через произведение чисел, получаемых последовательным извлечением квадратного корня из x. Таким образом,

x^1/3 = x^{1/2 – 1/4 + 1/8–1/16 + …} = x^{(1/2 – 1/4)}·x^{(1/8 – 1/16)}·… = x^1/4·x^1/16·…

Конечно, это произведение сходится достаточно медленно, но выполнять его очень просто и удобно. Например, найдем (51)1/3:

(51)^1/3≈(51)^1/4·(51)^1/16·(51)^1/64·(51)^1/128·… ≈ 2,6723·1,2786·1,0634·1,0155·… ≈ 3,6897.

Очевидно, что (3,6897)³ ≈ 50,2. Относительная погрешность этого вычисления составляет меньше 1,5%.

Отметим, что есть много разных других способов выполнить такое же вычисление. Например, метод последовательных приближений или метод касательных Ньютона.

Но другие методы требуют последовательного выполнения ряда алгебраических вычислений и лучшей математической подготовки.

Второй вопрос касается расчета значений известных тригонометрических функций типа sin (или cos) для любого значения угла, с помощью того же простейшего непрофессионального калькулятора.

Единственное, что мы будем считать известным, так это стандартные значения: sin(π/3), sin(π/4) и sin(π/6). Также учтём, что для углов α < π/12 можно воспользоваться с точностью лучше, чем 1,2 % известными ещё Эйлеру первыми членами разложения sin (или cos) sin α ≈ α (cosα ≈ 1), где α выражено в радианах (1 радиан ≈ 57,296º).

Любой угол от 0 до π/2 можно представить в виде α_р ± Δα, где α_р = 0, π/3, π/4, π/6, π/2, а Δα < π/12 = 15º.

Найдём, например, sin(69º) = sin(60º+9º) или в радианной мере sin(π/3+9/57,296) = sin(π/3 + 0,1571).

Далее

sin(π/3 + 0,1571) = sin(π/3) cos(0,1571) + sin(0,1571) cos(π/3) ≈

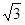≈ [/2]·1 + 0,1571·1/2 = 0,9445.

Аналогично, пользуясь формулой cos(α+β) = cosα·cosβ – sinα·sinβ для косинуса суммы двух углов, нетрудно найти косинус любого угла.

В заключение можно предложить тем, кто заинтересовался приведенными вычислениями, пару подобных задач.

1. Получите аналогичные выражения (то есть получите выражения через произведения квадратных корней) для корней других степеней, например, x^1/5, x^1/7 и т.п.

2. Найдите простой (лучше самый простой) способ нахождения квадратного корня из любого числа, используя операции «+», «–», «×», «:».

Желаю успехов,

А.М. Пальти, доцент, кафедра общей и теоретической физики Физико-математического факультета Национального технического университета «КПИ» им. И.Сикорского