С самого начала, хочу предупредить, пишу для тех, кто больше любит во-просы, чем ответы. Почему? Без вопросов нет прогресса и просто скучно. Конечно, не все вопросы мы будем оставлять без ответа.

Предмету нашего разговора много тысяч лет и, несмотря на это, он сохранил загадки, которые пока не имеют решения. А это доказывает его молодость и современность.

Что же это за такой сложный раздел математики, что его относят к высшей и в школе изучают только азы? Начнем с ответа на некоторые простые вопросы, касающиеся сути этого самого раздела, который называют математическим анализом.

Начнём издалека, с другого раздела, с геометрии, которую в школе изучают более подробно. Её истоки теряются в глубине веков, в древних Вавилоне, Египте, Греции. И начиналась эта наука с измерений земельных участков.

Но вот что интересно, если участок имеет простую прямоугольную форму, то такие участки нетрудно измерять и сравнивать. А как быть, если нет необозримых степных просторов, как у нас на Украине? А если земли мало, и участки имеют кривую границу. Как быть в этом случае? Как сравнить площади таких участков?

Или скажем, издревле использовали сосуды для разных напитков. Как сравнить их ёмкость, то есть объём, тоже важная задача, возникшая в незапамятные времена. Например, великий учёный Эллады, Архимед (III век до н.э.), кроме различных изобретений с использованием рычагов, зеркал или создания фортификационных сооружений, занимался расчётом объёма бочки с искривленной поверхностью.

Знаменитый своими апориями философ Зенон Элейский (V век до н.э.) по существу играл на непонимании понятия мгновенной скорости его современниками, как впрочем, и их потомками. Он, на полном серьёзе доказывал, что быстроногий Ахиллес не в состоянии обогнать неповоротливую черепаху.

Все эти, такие разные, задачи имеют нечто общее, имеющее отношение к предмету нашего разговора. Это общее – специальная операция. По существу, именно в ней таится отличие высшей математики от элементарной. Эта операция – предельный переход.

Об этом поговорим немного позже, а сейчас заметим, что в выражении «математический анализ» чего-то не хватает. Действительно, анализ чего? Какой объект имеется в виду? Оказывается, таким объектом является хорошо известное школьнику понятие функции или функциональной зависимости.

С её объяснения естественно начать наш разговор. Конечно, сегодня это понятие формулируется не совсем просто. Но мы начнём с определения, достаточного для наших целей. Оно возникло после длительной дискуссии с участием немецкого математика Лежена Дирихле и русского учёного Николая Ивановича Лобачевского.

Вообще надо заметить, что понятие функции претерпело большую эволюцию, и об этом можно прочитать в замечательной популярной книге Н.Я. Виленкина «Функции в природе и технике». Для наших целей достаточно определения, к которому учёные пришли после той самой дискуссии. Звучит оно так.

Переменная величина у называется функцией переменной величины х, если каждому значению величины х соответствует единственное значение величины у.

Это понятие лежит в основе нашего описания явлений природы и позволяет применять математику с пользой для человека.

В определении много недоговорок. Например, что значит «каждому значению величины» или «значение переменной величины»?

Что касается первого, надо знать не отдельные значения х, а все из некоторого множества. Это множество называют областью определения данной функции и обозначают {x}. Соответственно есть область значений функции – это тоже числовое множество, его обозначают {у}.

Что можно сказать об этих числовых множествах?

Различают вещественные числа (их начинают изучать уже в первом классе) и комплексные. Все ли вещественные числа могут быть значениями величины х? Если нет, то какие могут, какие нет? В определении об этом ничего не говорится. И это понятно, поскольку это зависит как от природы функции, так и от задач, в которых её используют.

Например, функцию х! (по крайней мере, в элементарной математике) рассматривают для целых положительных х, записывают её обычно n! = 1·2·3·…·n. Функцию lg x только для х > 0. Есть примеры более сложных множеств {x}.

В подавляющем большинстве случаев областью определения функции служит «отрезок» (закрытый или открытый) – совокупность всех вещественных чисел, заключённых между двумя заданными числами (иногда это вся прямая или полупрямая х > 0).

Для функций математического анализа областью, где проявляются их индивидуальные черты, необходимые в практических применениях, является совокупность всех вещественных чисел. Это множество называют континуумом.

Поэтому серьёзное изучение математического анализа обычно начинают с континуума и изучают его серьёзно на математических факультетах университетов.

Здесь мы скажем совсем немного о том, что же такое континуум? Какого типа вещественные числа существуют? Мы знаем, что в школе изучают рациональные числа. Это целые числа и дроби, как положительные, так и отрицательные. Но ещё в школе Пифагора знали, что этих чисел недостаточно.

Например, нет рационального числа, равного 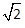, то есть числа, квадрат которого равен 2. А зачем нужно иметь такое число? Хотя бы потому, что длина диагонали квадратного участка со стороной 1 м, как раз равна  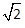м.

Нетрудно доказать, что 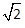 нельзя представить в виде p/q, где p и q – целые числа. И это вполне по силам школьнику, попробуйте это сделать.

Числа, подобные 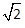, называют алгебраическими. Связано это с тем, что такие числа появляются как решения алгебраического уравнения конечной степени с целыми коэффициентами.

Итак, в континууме присутствуют алгебраические числа. Где среди рациональных чисел они находятся? Как производить арифметические действия с таким числами? Например, что такое 1 + ?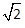

Понятно, что таких чисел много и они ничем не хуже рациональных. К ним относятся, например, решения алгебраического уравнения вида qхⁿ – p = 0.

Интересно, что операции над алгебраическими числами всегда приводят к таким же числам. Но оказывается, для математического анализа даже алгебраических чисел недостаточно.

И вот теперь мы вплотную подходим к упомянутой выше операции предельного перехода.

Так вот, упомянутая предельная операция привела к возникновению чисел нового типа. Их назвали трансцендентными.

Примером таких чисел является знаменитое число π ≈ 3,14, которое появилось очень давно. Оно равно отношению длины окружности к её диаметру.

Не менее известное другое число – основание натуральных логарифмов е ≈ 2,71. Это число имеет огромное количество применений в технике, например, при описании затухающих колебаний.

Множество, которое включает все типы известных чисел, обеспечивающих потребности практики, как раз и назвали континуумом.

Какое же отношение имеют упомянутые выше задачи нахождения площади участка с криволинейной границей или объёма бочки к предельной операции. И как решать подобные задачи?

Общий подход такой. Легко найти площадь квадрата или объём кубика. Тогда естественно сложную фигуру разбить на маленькие квадратики или кубики и найти искомую площадь или объём, как сумму таких простых элементарных фигур. При этом результат будет тем точнее, чем мельче разбиение сложной фигуры на элементарные. Точное значение, например площади, получим, как предел суммы, если площадь отдельного элементарного квадратика устремить к нулю.

Другой пример даёт длина окружности, которую можно рассматривать как предел периметра вписанного в окружность правильного многоугольника, при стремлении числа его сторон к бесконечности. Считать, что такого предела не может быть, значит отрицать существование длины окружности.

В принципе, было бы неплохо иметь способ построения любых вещественных чисел, входящих в континуум, из хорошо понятных нам рациональных чисел. Часто так и поступают. А делают это с помощью операции предельного перехода или, короче, предела.

Например, упомянутое число 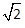 не является рациональным, но его можно представить как предел последовательности приближающихся к нему рациональных чисел 1,4   1,41   1,414   1,4142   1,41421   1,414213 ... Дальше при изложении математического анализа строят континуум, например, на основе понятия сечения множества вещественных чисел. Его предложил немецкий математик Рихард Дедекинд.

Отложим интересный рассказ об общей теории континуума, которая лежит в основе всей теории действительных чисел. Это – отдельный разговор.

Вернёмся к математическому анализу, точнее перейдём к его главным понятиям, таким, как производная (простой пример, предел отношения пути ко времени, это мгновенная скорость) и интеграл (пример, описанное выше определение площади). Очевидно, эти операции основаны на специальных видах предела.

Скажем пару слов о применениях математического анализа. Об этих применениях можно рассказывать очень долго. Для простого их перечисления не хватит не только статьи, но даже толстой книги.

Например, расчёт работы двигателя внутреннего сгорания или холодильника, реактивного самолёта или ракеты невозможен без теоретических расчётов, основанных на математическом анализе и последующих более сложных разделах высшей математики.

Иногда, в связи с приоритетом создания математического анализа, вспоминают знаменитые имена Исаака Ньютона и Готфрида Лейбница. Несомненно, вклад этих учёных в создание математического анализа неоценим.

Но мы видели, что задачами математического анализа занимались ещё в древней Греции. Да и в средние века многие учёные, например, учитель Ньютона Исаак Барроу, сделали свой существенный вклад в интегральное и дифференциальное исчисление (ещё одно название обсуждаемого раздела математики).

Чтобы стало понятно, уточним. Вклад упомянутых учёных состоял в таком упорядочении накопленных знаний, при котором решать сложные задачи стало намного проще. Не требовались длинные вычисления и многие годы на расчёты. Так стало проще находить корни алгебраических уравнений 3-й и 4-й степени, после получения общих формул их решения.

После того, как физик Ричард Фейнман придумал свои диаграммы, он за считанные дни решил сложнейшую задачу квантовой теории поля, на которую другие теоретики тратили многие месяцы.

Закончим наш краткий экскурс в высшую математику одним загадочным парадоксом и возникающим в связи с этим вопросом.

Если вы посмотрите в одном из предыдущих выпусков нашего журнала статью, посвящённую погрешностям косвенных измерений, то увидите там соображения уважаемого профессора МФТИ Д.В. Сивухина о производной.

Там же поставлен вопрос: насколько правильно применять понятие производной при расчёте погрешности?

Расширим постановку этого вопроса. Основа физики – эксперимент, измерения. Выполняются эти измерения с определённой точностью. Для определения погрешности косвенных измерений используют формулу с производными.

Но, в соответствии с замечаниями профессора, «предельный переход Δx → 0, вводимый в математике при определении производной», недопустим при анализе экспериментов. То есть, использовать производные для определения погрешностей нельзя?..

Возникает естественный вопрос, какие есть основания применять математический анализ с его производными в физике? Точнее, как применять его при анализе данных опыта?

А.М. Пальти, старший научный сотрудник по физике ВТСП