ИСТОРИЧЕСКИЕ АСПЕКТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА

Понятие функции имеет давнюю историю. Первые шаги на длинном пути создания общего понятия функции сделали математики Древнего Вавилона. Они составили таблицы обратных значений чисел, их квадратов и кубов, сумм квадратов и кубов чисел. В современном понимании это были таблицы значений таких функций: y = 1/x, y = x², y = x³, y = x²+ x³.

С их помощью можно было решать и обратные задачи. Составляли они и таблицы значений функций двух переменных, например, таблицы сложения и умножения.

Математики Древней Греции решили некоторые задачи на наибольшее и наименьшее значения, открыли соотношение между длинами хорд и диаметров.

Греческие астрономы заложили основы новой области математики – тригонометрии. Они составили таблицы зависимости между мерами дуг и длинами хорд, их стягивающих.

По сути, это уже были таблицы значений функции y = 2sin(x/2) .

Впоследствии математики исследовали и много других функциональных зависимостей, хотя самого понятия функции ещё не вводили. Даже в трудах Р. Декарта, П. Ферма, И. Ньютона и Г. Лейбниц понятие функции носило, по сути, интуитивный характер и связывалось с геометрическими или механическими представлениями.

Путь к первому определению функции проложил французский математик Рене Декарт (1596–1650), введя понятие переменной величины.

Термин «функция» впервые предложил в 1692 г. выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646–1716) для характеристики различных отрезков, соединяющих точки некоторой кривой.

Сначала понятие функции использовали в очень узком смысле, связывая только с геометрическими образами. Речь шла об отрезках касательных к кривым, их проекциях на оси координат и другие линии, которые выполняют для данной фигуры некоторую функцию (от латинского функтус – выполнять). Таким образом, понятие функции на то время ещё не было освобождено от геометрической формы.

Лишь в 1718 г. швейцарский математик Иоганн Бернулли (1667–1748) сформулировал определение функции, свободное от геометрического языка: «Функцией переменной величины называется количество, образованное каким угодно способом из этой переменной величины и постоянных».

Отход от геометрических образов знаменовал новую эпоху в изучении функций.

Определение И. Бернулли опиралось не только на работы Г. Лейбница и его школы, но и на исследования И. Ньютона, который изучил много разных функциональных зависимостей и их свойства. Вместо слова «функция» И. Ньютон использовал термин «ордината». Он сводил изучение геометрических и физических зависимостей к изучению этих «ординат», а сами «ординаты» описывал разнообразными аналитическими выражениями.

Чтобы определение функции, данное И. Бернулли, стало полноценным, нужно было договориться, какие способы задания функций можно считать допустимыми. Обычно считали, что допускаются функции, заданные выражениями, в которые входят числа, буквы, знаки арифметических действий, возведение в степень с целым показателем и извлечение корней. Рассматривали также тригонометрические, обратные тригонометрические, показательные, логарифмические функции.

Такие функции называли элементарными функциями.

Леонард Пауль Эйлер (1707–1783), выдающийся математик швейцарского происхождения, вся научная карьера которого связана с Россией и Германией, в своём трактате «Дифференциальное исчисление» (1755 г.) уточнил и обобщил определение И. Бернулли.

А именно, Л. Эйлер писал: «Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подлежат изменению, то первые называются функциями вторых». Хотя в одной из своих работ Л.Эйлер даже рассматривал график функции как кривую, которая начертана «свободным движением руки».

Труды Л. Эйлера сыграли важную роль в освобождении математического анализа от языка геометрии и механики. В них впервые теория тригонометрических функций была изложена без обращения к геометрии, а показательная и логарифмическая функции стали равноправными с алгебраическими функциями.

Л. Эйлер подчёркивал, что математический анализ является наукой о функциях, что «весь анализ бесконечно малых вращается вокруг переменных количеств и их функций». Л. Эйлеру принадлежит ввод символа функции f(x).

В связи с таким взглядом Л. Эйлера на функцию, между ним и его соперниками, в частности, с известным французским математиком Жаном Лероном Д'Аламбером (1717–1783), возникла полемика вокруг возможности аналитического выражения произвольной кривой и о том, которое из двух определений (кривая или формула) следует считать более общим. Возник также спор о том, можно ли одну функцию задавать несколькими аналитическими выражениями.

Разъяснения внёс французский математик Жан Батист Фурье (1768–1830). В представленных им в Парижскую Академию наук в 1807 и 1811 гг. мемуарах по теории распространения тепла в твёрдом теле были приведены первые примеры функций, заданных на различных промежутках различными аналитическими выражениями.

Это так называемые «кусочно-заданные функции», которые в настоящее время широко применяются как в теоретических исследованиях, так и на практике.

Из трудов Ж. Фурье следовало, что любую кривую, независимо от того, из скольких и каких разнородных частей она составлена, можно представить в виде единого аналитического выражения. Также Ж. Фурье установил, что существуют разрывные функции, которые можно записать аналитическим выражением.

Выводы Ж. Фурье обосновал в своём трактате «Курс алгебраического анализа» (1821 г.) – французский математик Огюстен Луи Коши (1789–1857).

Дальнейшее развитие математического анализа и практических применений математики привело к расширению понятия функции. В 1834 г. выдающийся русский математик Николай Иванович Лобачевский (1792–1856) сформулировал определение функции, в основу которого была положена идея соответствия: «Общее определение требует, чтобы функцией от x называть число, которое даётся для каждого x и вместе с x постепенно меняется. Значение функции может быть задано или аналитическим выражением, или условием, которое даёт средство проверять все числа и выбирать одно из них; или, наконец, зависимость может существовать и оставаться неизвестной...».

Аналогичную точку зрения на понятие функции ещё раньше высказал чешский математик Бернард Больцано (1781–1848). К сожалению, его научный труд «Учение о функции», написанный в 1830 г., был напечатан лишь через сто лет, уже после смерти талантливого математика.

В 1837 г. немецкий математик Петер Густав Лежен Дирихле (1805–1859) сделал такое обобщение понятия функции: «y есть функция переменной x (на отрезке a ≤ x ≤ b), если каждому значению x соответствует определённое значение y, причём не имеет значения, каким образом установлено это соответствие – аналитической формулой, графиком, таблицей или даже просто словами».

Примером, что соответствует этому общему определению, может быть так называемая функция Дирихле:

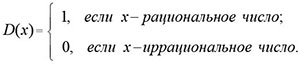
Во второй половине XIX в. после создания теории множества в определение функции, кроме идеи соответствия, было привлечено ещё и идею множества, а потому определение функции стали формулировать так: «Если каждому элементу x множества X поставлен в соответствие некоторый определённый элементy y множества Y, то говорят, что на множестве X задана функция y = f(x)». Иногда говорят, что множество X отображается в множество Y по закону f.

Такое определение функции можно применять не только к величинам и числам, но и к другим математическим объектам, например, геометрическим фигурам.

Однако математический анализ XIX века ограничивался исследованием только числовых функций, то есть таких, область определения и множество значений которых - числовые множества. Таким образом, математический анализ XIX века продолжал основываться на определении Дирихле.

Но уже в начале ХХ века возникла необходимость дальнейшего расширения понятия функции, вызванная потребностями физики. Особенно острой она стала после издания в 1930 г. монографии «Основы квантовой механики», которую написал английский физик Поль Адриен Морис Дирак (1902–1984).

П. Дирак ввёл понятие так называемой «дельта-функции», которая выходила далеко за пределы классического определения функции.

По определению П. Дирака, дельта-функция – это функция y = δ(x), равная нулю при всех x, кроме x = 0, где дельта-функция превращается в бесконечность, причём .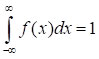

В связи с этим в 30–40 гг. ХХ в. советский математик Николай Максимович Гюнтер (1871–1941) и другие учёные издали труды, в которых рассматривали не «функции точки», а «функции области», что лучше соответствовало физической сущности квантово-механических явлений.

Дальнейшие научные исследования привели к понятию «обобщённой функции», которое охватывает и дельта-функцию. Основной вклад в разработку теории обобщённых функций внесли французский математик Лоран Шварц (1915–2002) и выдающийся советский математик Сергей Львович Соболев (1908–1989).

Свою теорию обобщённых функций С.Л. Соболев предложил в 1935 г. Через 10 лет к аналогичной идее независимо пришёл и Л. Шварц, который связал вместе все предыдущие подходы и предложил удобный формализм, основанный на теории топологических векторных пространств.

Л.Шварц построил теорию преобразований Фурье обобщённых функций, которой у С.Л. Соболева не было. Однако считается, что именно С.Л. Соболев является первооткрывателем обобщённых функций.

Следует отметить, что важный вклад в развитие теории обобщенных функций внесли советские математики Израиль Моисеевич Гельфанд (1913–2009) и Георгий Евгеньевич Шилов (в начале научной карьеры известный как Юрий Боссе; 1917–1975) и другие.

Итак, понятие функции продолжает развиваться и расширяться в соответствии с потребностями развития математической науки и её практических применений.

(Продолжение следует)

Н.В. Шмигевский, кандидат физико-математических наук