Начало в №8, 2021

Что такое число, какие бывают числа, для чего они служат, какие свойства они имеют. Изложение материала ведётся полуформально, и мы просим извинения у тех людей, которые любят строгость и формализм.

3. РАЦИОНАЛЬНЫЕ ЧИСЛА

Из сказанного выше следует, что множества натуральных и целых чисел незамкнутые относительно операции деления. Операция деления может привести к дробным числам, как, например, 4/3, 7/5, –5/4 и т.д. Совокупность всех этих дробей называется множеством рациональных чисел. Итак, произвольное рациональное число можно представить в виде a/d, где a и d – целые числа, причём d ≠ 0. Рассмотрим следующие случаи:

1).   

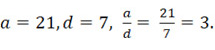
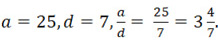
В нашем примере d является делителем числа 21 в смысле определения, данного в предыдущем разделе, то есть 7 – точный делитель числа 21. А во втором примере 7 не является точным делителем числа 25. Если назвать 25 делимым, а 7 – делителем, то мы получаем (неполное) частное 3 и остаток от деления 4. Итак, делитель используется здесь в более общем смысле и применяется к большему числу случаев.

2). Отметим, что выражения «рациональное число» и «рациональная дробь» являются синонимами, хотя само по себе слово дробь используется для обозначения произвольного выражения, состоящего из числителя и знаменателя, как, например, .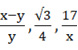

3). В определение рационального число входят слова «число, которое можно представить в виде a/d», где a, d – целые числа, d ≠ 0. Почему его нельзя заменить словами «число вида a/d, где a, d целые числа, d ≠ 0»? Причиной является то, что существует бесконечно много способов представления одной и той же дроби, например, 2/3, 4/6, 8/12, 10/15, или -2/-3, -10/-15 и т.д. Дробь определяется так, что её значение не меняется при умножении числителя и знаменателя на одно и то же число. Но не всегда легко определить для данной дроби, является или нет она рациональным числом.
Например, дроби  являются такими: первая из них рациональное число, поскольку

,

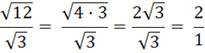и получаем дробь a = 2, d = 1; а вторая рациональным числом не будет, поскольку

,

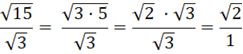а √2 (как будет показано далее) рациональным числом не является.

4). Отметим, что произвольное целое число n будет рациональным, так как n=n/1, и, следовательно, a = n, d = 1.

5). Какая же дробь выбирается для работы, из класса дробей, которые ей равны (эквивалентны)? Из предыдущего пункта 3) следует, что представление дроби следует выбирать таким, в котором числитель и знаменатель не имеют общих делителей (такие числа, которые не имеют общих делителей, называются взаимно простыми).

3.1. Изображение рациональных дробей

Хорошо известным является изображение рациональных чисел не в виде 1/2, 2/4, 3/6 и т.д., а в виде десятичных дробей. Например, число 1/2 представляется десятичной дробью 0.5, а числа 2/5 = 0,4, и 1/80 = 0,0125, в то время как десятичные дроби других чисел бесконечны:

1/3=0,133333…, 1/6=0,1666…, 5/11=0,454545….

Итак, возникает вопрос, какие рациональные дроби имеют конечное десятичное представление, а какие имеют бесконечное десятичное представление? Рассмотрим конкретные примеры. Возьмём конечную десятичную дробь 0,8625. Мы знаем, что 0,8625=8625/10000, и произвольную конечную десятичную дробь можно представить со знаменателем 10, 100, 1000 или какой-либо степенью числа 10. Упрощая дробь до несокращаемой, получаем:

0,8625=8625/10000=69/80.

Знаменатель 80 имеет разложение на простые множители: 80 = 2⁴ ∙ 5, как и разложение 100000 = 2⁴ ∙ 5⁴. Эти два разложения имеют общие простые множители 2 и 5, и, если начинать не с 0,8625, а с произвольной другой конечной дроби, то несокращаемая дробь тоже будет иметь это же свойство. Иными словами, в разложении знаменателя на простые множители могут входить только простые числа 2 и 5, поскольку знаменатель является делителем некоторой степени числа 10, а 10 = 2 ∙ 5. Это обстоятельство, оказывается, является определяющим, а именно, имеет место такая теорема.

Теорема 2. Несокращаемая рациональная дробь a/b имеет конечное десятичное представление тогда и только тогда, когда число b не имеет простых делителей, отличных от  2 и 5.

Заметим, что число b не обязательно должно иметь среди своих простых делителей оба числа 2 и 5, или не делиться на них совсем; оно может делиться только на одно из них. Действительно, 1/25=0,04, 1/16=0,0625, 7/1=7,0, где b = 25, 16, 1.

Покажем, что когда b не имеет других простых делителей, кроме 2 и 5, то дробь a/b имеет представление в виде конечной десятичной дроби.

Пусть b = 2^m ∙ 5ⁿ  есть разложение числа b  на простые множители. Рассмотрим случаи:

a) m < n. Помножим знаменатель и числитель дроби a/b на 2^n-m:

и мы получим конечную десятичную дробь, где d = a ∙ 2^m-n  .

b) n ≤ m. Помножим знаменатель и числитель дроби на 5^n-m:

,

где d = 2 ∙ 5^m-n.

3.2. Периодические десятичные дроби

Рациональные дроби мы разделили на два класса – на те, которые представляются конечными десятичными дробями, и те, которые не представляются такими дробями. Покажем, что произвольная дробь из второго класса будет иметь периодическую часть, которая повторяется. Например,

5/11=0,454545… и 3097/9900=0,312828282…

Периодическую часть дроби заключают в круглые скобки, и тогда:

5/11=0,(45); 3097/9900=0,312(82); 1/3=0,(3).

Причина периодичности становится понятной, если выполнять деление в столбик. Например, рассмотрим перевод рациональной дроби 2/7 в десятичную дробь:

После получения остатка 2, весь процесс деления повторится, поскольку он начинался с деления числа 2. Таким образом, получаем:

2/7=0,(285714).

В рассматриваемом примере повторение проявилось, когда деление 2 на 7 встретилось второй раз. Повторение вовсе не обязательно возвращает нас к первому шагу. Например, разложение в десятичную дробь рациональной дроби 209/700 приобретает вид:

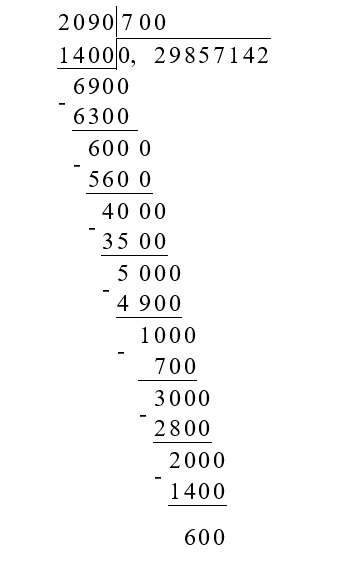
Тут повторение возникло, когда появился остаток 600, который встречался несколькими шагами ранее, следовательно, 209/700=0,29(857142).

Общий случай произвольной дроби a/b рассматривается аналогичним способом. При делении целого числа a на целое число b остаткам могут быть только такие числа: 1, 2, ..., b-2, b-1. Поэтому в процессе деления обязательно возникает повторение остатка. С этого момента начинается новый цикл, результатом которого является периодическая десятичная дробь.

Таким образом, нами доказана первая часть следующего утверждения.

Утверждение 3. Произвольное рациональное число a/b представляется в виде конечной десятичной дроби или бесконечной периодической десятичной дроби. Напротив, произвольная конечная десятичная дробь или бесконечная периодическая десятичная дробь является некоторым рациональным числом.

Вторая часть этого утверждения, которое нам нужно доказать, касается двух классов десятичных дробей – конечных и бесконечных периодических. Конечные десятичные дроби, как это было показано выше, являются рациональными числами. Рассмотрим бесконечные периодические десятичные дроби. Начнём с конкретного примера десятичной периодической дроби:

x = 28,123(456), или в другом виде x = 28,123456...

Помножим эту дробь на одно число, а потом на другое число так, чтобы при вычитании одного произведения из другого бесконечная периодическая часть сократилась. В нашем случае такими числами являются 10⁶ и 10³, поскольку

10⁶ ∙ x = 28,123456.(456) и 10³ ∙ x  = 28,123.(456),

так что разность 10⁶ ∙ x -  10³ ∙ x   равняется 999000 ∙ x = 28095333.
Следовательно, x = 28095333/999000 является рациональным числом.

Теперь можно обобщить этот способ и получить доказательство второй части утверждения 3.

Покажем сначала, что множители 10³ и 10⁶ выбираются не произвольно, а на основании определённого правила. Поскольку целая часть десятичной дроби не влияет на общий результат, то наши десятичные дроби будут иметь далее вид , где a₁, a₂,…, a_j  означает s последовательных цифр, части, что не повторяются, а b₁, b₂,… b_t – t цифр периода десятичной дроби x. В рассмотренном выше примере было

s = 6, t = 3, a₁ = 1, a₂ = 2,  a₃ = 3 = b₁ = 4, b₂ = 5, b₃ = 6.

Если x умножить сначала на 10^{s + t}, а затем на 10^s и второе произведение вычесть из первого, то получаем

,
,
.

Отсюда находим

.

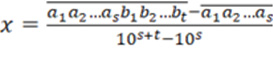Следовательно, число x является отношением двух целых, и поэтому оно рациональное число.

3.3. Представление конечной десятичной дроби в виде периодической десятичной дроби

Выше было показано, что рациональные числа могут быть представлены в виде конечных десятичных дробей или бесконечных периодических десятичных дробей. Оказывается, что второе представление более общее, поскольку произвольную конечную десятичную дробь можно представить бесконечной периодической дробью. Сделать это можно совершенно очевидным способом, добавляя число 0 в периоде. Например, 3,7 = 3,7000 ... = 3,7(0). Но существует другой способ такого перевода, который менее очевиден. Начнем с известного разложения 1/3 = 0,33333….

Если обе части этого равенства домножить на 3, то в результате получаем несколько странное равенство:

1 = 0,99999…

(3)

Следовательно, имеем равенство между конечной десятичной дробью 1 или 1,0 и бесконечной периодической дробью 0,99999… .

Рассмотрим соотношение (3) следующим образом. Обозначим бесконечную дробь 0,99999... неизвестным x, то есть

x = 0,99999…

(4)

Домножим обе части (4) на 10, получим
          10x = 9.9999… = 9 + 0.9999…

Вычитая отсюда (4), получаем

              9x = 9,  или x = 1.

Итак, равенство (3) доказано.

Поделим равенство (3) на 10, 100, 1000, 10000 и т.д., находим

0.1 = 0.099999… , 0.01 = 0.0099999… , 0.001 = 0.00099999… , 0.0001 = 0.000099999… и т.д.

(5)

Эти соотношения можно применить для перевода произвольной конечной десятичной дроби в бесконечную периодическую десятичную дробь.

Например,                       

3.8 = 3.7 + 0.1 = 3.7 + 0.99999 = 3.7(9) .
0.728 = 0.727 + 0.001 = 0.727 + 0.00099999… = 0.727(9).

Наоборот, равенства (3) и (5) позволяют преобразовать бесконечную периодическую дробь в конечную десятичную дробь:

0.36999… = 0.36 + 0.00999… = 0.36 + 0.01 = 0.37;
11.0999… = 11 + 0.0999… = 11 + 0.1 = 11.1.

Опять возникает вопрос: сколько представлений имеет рациональное число в виде бесконечной периодической дроби? Действительно, число 0.43, кроме записи 0.42999, можно представить в виде

0.430, 0.4300, 0.43999, … . 

Поэтому, когда речь заходит о представлении рационального числа в виде бесконечной десятичной дроби, то имеем в виду не

0.43000…, а 0.42999… .

---

[1] Пифагорейцы – представители школы Пифагора.

(Продолжение в следующем номере)

С.Л. Крывый, д.ф.-м.н., профессор;
В.П. Шевченко, к.ф.-м.н., доцент;
Киевский национальный университет имени Траса Шевченко

 

По теме:

Числа и вычисления