
В конце 1879 года двадцатипятилетний горный инженер Анри Пуанкаре, совсем недавно защитивший докторскую диссертацию в Сорбонне, был приглашён читать лекции по математике в Канском университете.
Ещё в начале года Анри испытал глубокое потрясение: в результате обвала на шахте погиб его друг, с которым он вместе работал после окончания Горной школы. Случайность спасла Анри от такой же участи: в тот день он не спускался в забой, поскольку по распоряжению начальства был оставлен на поверхности для решения текущих дел.
Анри не без колебаний дал согласие на предложенную ему преподавательскую работу, поскольку задатков лектора он в себе не ощущал. Но зато лекционная работа, которая не должна была отнимать много сил, сулила свободное время для научной работы.
По приезду в Кан – торговый центр в Нормандии – Пуанкаре первым делом решил ознакомиться с городом. Город, расположенный на Северо–Западе Франции на реке Орн, был знаменит крупной библиотекой, университетом, морским портом и двумя монастырями: женским с церковью Троицы и мужским с церковью Сент Этьен.
И чем ближе Анри знакомился с городом, сохранившим свой средневековый облик со сплетением плавно искривлённых улиц с двухэтажными каменными домами, с церквями, построенными еще в XI веке, тем большую приязнь он испытывал к месту, где ему предстояло теперь работать.
Особенность натуры Пуанкаре состояла в том, что чем сильнее он погружался в свой внутренний мир, тем окружающий мир как бы переставал для него существовать: он не ощущал голода и смены погоды, не реагировал на обращения к нему близких людей.

Историки причисляют Анри Пуанкаре к величайшим математикам всех времён. Он считается, наряду с Гильбертом, последним математиком-универсалом, учёным, способным охватить все математические результаты своего времени. Его перу принадлежат более 500 статей и книг. «Не будет преувеличением сказать, что не было такой области современной ему математики, „чистой“ или „прикладной“, которую бы он не обогатил замечательными методами и результатами»
Вот один из таких случаев. Анри был приглашён встретить наступающий 1880–й год в дом своих друзей. Поскольку Анри был одинок, он с благодарностью принял приглашение. Но его поведение озадачило всех присутствующих на вечеринке: весь вечер Анри провел в молчании: прохаживаясь по комнатам, он ни с кем не вступал в беседу. Когда же ему осторожно напомнили, что наступил новый год, он, на мгновенье очнувшись, поблагодарил за сообщение и продолжил свои размышления.
Над чем же так упорно размышлял Анри Пуанкаре? Вспомним, что он был не только горным инженером, но, в первую очередь, математиком.
К моменту приезда в Кан он бился над проблемой, связанной с решением определённого класса дифференциальных уравнений. Проходили дни упорного умственного труда, но ни к какому результату он прийти не мог.
Что произошло с ним дальше, Пуанкаре поведал спустя много лет в своих воспоминаниях.
Утомлённый безрезультатным поиском решения задачи, Анри решил взбодрить себя и сварил вечером чашечку черного кофе, который, как оказалось позже, явился чудодейственным лекарством для его мозга.
Кофе не позволил ему заснуть, и он провел ночь, полную кошмаров. Совершенно обессиленный, Анри только под утро забылся поверхностным сном.
Каково же было его удивление, что с пробуждением в его мозгу как бы независимо от его воли возникло чёткое, не вызывающее никаких сомнений решение, над которым он так долго безуспешно бился в дневные часы размышлений.

(1833 – 1902)
– немецкий математик. Основные исследования по
теории линейных дифференциальных уравнений
с аналитическими коэффициентами, все решения
которых обладают только т. н. регулярными особыми
точками (уравнения классов Фукса).
Открыл перемещающихся особых точек (1884).
Создал научную школу в области
линейных дифференциальных уравнений.
В его, теперь уже контролируемом сознании, отчётливо обозначились функции, которые он позже назовет фуксовыми (в честь математика Фукса, чья работа натолкнула его на правильное решение), позволяющие интегрировать линейные дифференциальные уравнения в комплексной плоскости.
Анри немедленно сел за стол, записал подсказанный ему подсознанием результат, и приступил к доказательству.
Потребовалось всего несколько часов работы и бесспорное доказательство правильности результата, найденного им интуитивным путем, было получено.
Через несколько дней Пуанкаре написал Фуксу письмо: «... Функции, которые вы определили, обладают весьма замечательными свойствами, и так как я намерен опубликовать полученные мною результаты, прошу вашего разрешения дать им имя фуксовых функций, поскольку это вы их открыли…».
Благосклонное согласие Фуксом было дано: так функции, в рождении которых сам Пуанкаре сыграл не меньшую роль, получили название фуксовых.
В последующие годы своего научного творчества Пуанкаре не раз анализировал этот и другие подобные случаи получения интуитивным путем правильного результата по проблемам, над которыми он долго до того безуспешно бился в часы бодрствования.
Много лет спустя в зените известности, будучи приглашённым на заседание «Психологического общества» в Париже, Пуанкаре поделился с присутствующими самым потаённым – итогом своих размышлений над тем, как мыслит математик.
Через некоторое время он опубликовал содержание своего доклада в книге «Учёный и наука». Вот как по Пуанкаре выглядит «технология» мышления математика (от себя добавим – успешного математика), включающая три основные стадии или фазы.
Первая фаза: сознательная упорная работа над проблемой, рассмотрение её с разных сторон; мыслительная работа, не приводящая, однако, к конечному успешному результату.
Вторая фаза: подсознательная работа разума, связанная с поиском правильного результата среди множества различных вариантов, и передачей найденного решения в область сознательного. Таинственность этой фазы бесспорна, ибо не ясен ни механизм перебора множества вариантов, ни поиск истины, ни переход через порог, отделяющий область бессознательного от сознательного.
Третья фаза: сознательная работа, связанная с логическим доказательством интуитивно найденного решения.
В короткой форме три названные фазы мышления одарённых людей, размышляющих над решением различных проблем, можно выразить так: осмысление – озарение – доказательство.
Уместно заметить, что подобная «технология» открытий в математике была присуща и другим учёным.
Так, например, академик Владимир Андреевич Стеклов (1863 – 1926) в воспоминаниях о своём учителе и близком друге, выдающемся русском математике академике Александре Михайловиче Ляпунове (1857 – 1918), сообщает почти то же самое, что Пуанкаре писал о себе.
Ляпунов, по словам Стеклова, многие из полученных им результатов угадывал до того, как ему удавалось найти убедительное им доказательство.
Стеклов пишет: «Часто на вопрос, каким образом он пришёл к новым выводам, к новым неизвестным до сих пор обобщениям, Ляпунов отвечал: “Пока не знаю; я уверен, что это так, и постараюсь это доказать”. И впоследствии действительно доказывал».
Но вернемся к Пуанкаре, который обладал исключительно сильным интеллектом и решил много проблем в разных областях математики и физики.

В расцвете творчества Анри Пуанкаре сам систематизировал результаты своих обширных исследований, издав довольно объёмное «Математическое резюме».
Одна из проблем, вошедших в этот труд, касается геодезической линии, как составной части топологии – науки, изучающей свойства фигур, не изменяющихся при любых деформациях.
Топология является теоретической базой многих прикладных наук, в том числе геодезии, занимающейся точными методами измерения фигуры и размеров Земли и земной поверхности, а также отображения их на картах.
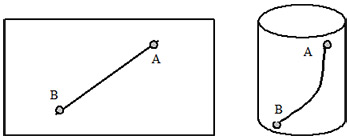
Кратко остановимся на понятии «геодезическая линия» – проблеме, которой Пуанкаре посвятил несколько фундаментальных работ. Проведём такой простой эксперимент. Возьмем лист бумаги, обозначим на нём точки А и В и проведём между ними прямую линию (рис. 2).
Теперь свернем листок в трубочку. Нанесённая на листке прямая линия АВ, проходящая теперь по поверхности цилиндра, искривляется.
Таким образом, если на плоской поверхности кратчайшее расстояние между двумя точками А и В есть прямая линия, то на поверхности цилиндра – кривая АВ, которая и есть геодезическая линия.

Материальная точка, остающаяся на поверхности при отсутствии других внешних сил движется по геодезической линии. Такую же форму принимает упругая нить, натянутая на поверхности.
Понятие «геодезическая линия» имеет прямую связь со многими проблемами хозяйственного назначения. Пусть, например, между двумя городами необходимо проложить газовый трубопровод или волоконно-оптический кабель. Если местность позволяет, то лучше всего их проложить вдоль геодезической линии, как кратчайшей и потому сулящей определённую, порой и немалую, экономию в расходовании материалов и сил.
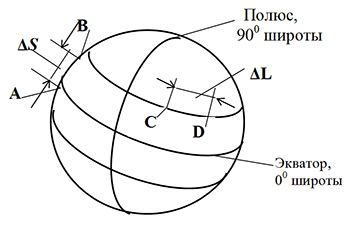
Обратимся теперь к модели формы Земли, представляющей собой эллипсоид, опутанный сетью геодезических линий: меридианами, соединяющими Северный и Южный полюса, и параллелями – окружностями, параллельными экватору (рис.3).
Эллипсоид описывается следующим алгебраическим уравнением:
|
|
(1) |
где а – большая полуось, с < a – малая.
У модели Земли а=6378,245км, с=6356,863км и, следовательно, полярное сжатие эллипсоида и эксцентриситет:
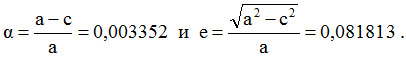
Рассмотрим случай, когда точки А и В расположены на одном меридиане, являющимся для них геодезической линией (рис. 4).
В этом случае длина геодезической линии между этими точками определяется с помощью интеграла, называемого эллиптическим:
|
|
(2) |
Θ1, Θ2 – широта точек А и В, расположенных на общем меридиане.
Решение интеграла (2) есть функция:
|
|
(3) |
ΔΘ – разность в градусах по долготе между точками A и B , Θ0 – широта в градусах.
Длина геодезической линии между точками С и D (рис. 4), расположенными на одной и той же параллели:
|
|
(4) |
ΔΘ – разность в градусах по долготе между точками C и D, расположенными на одной параллели; Θ – широта в градусах.
Результаты расчета по формуле (3) длины части меридиана ΔS в км при ΔΘ = 1° и по формуле (4) длины части параллели ΔL в км при Δ=1° при разных значениях широты Θ0 приведены в таблице 1.
Таблица 1
| Θ0, град. | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| ΔS, км | 110,576 | 110,599 | 110,663 | 110,762 | 110,883 | 111,012 | 111,134 | 111,234 | 111,321 |
| ΔL, км | 111,321 | 109,641 | 104,649 | 96,488 | 85,395 | 71,697 | 56,801 | 38,187 | 19,394 |
Задание.
Рассчитайте по формулам (3) и (4) длину геодезической линии при её протяженности Δ Θ = 20.
В.И. Каганов, доктор технических наук, профессор МИРЭА



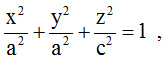
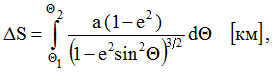
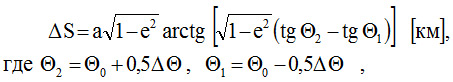
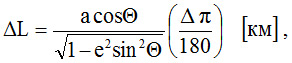






 Основатель и издатель
Основатель и издатель Copyright © 2016–2021 Научно-популярный
Copyright © 2016–2021 Научно-популярный