Продолжение. Начало в №1, 2018.

Часть 2

Мы раскритиковали известный метод расчёта погрешности косвенного измерения. А как же нужно рассчитывать эту погрешность? Чтобы дать вариант ответа на этот вопрос, обратимся к одному из важнейших в физике положений, – принципу наблюдаемости.

Значимость прямых измерений подтвердил Альберт Эйнштейн, когда задал себе вопрос: зависит ли понятие одновременности от того, движемся мы или нет? Он предложил свой знаменитый мысленный эксперимент со светом в качестве носителя информации о времени, когда произошло событие. Следствия опыта легли в основу специальной теории относительности.

При создании этой теории Эйнштейн сформулировал принцип наблюдаемости. Любое понятие, используемое в физике, должно быть подкреплено реальным или воображаемым, но потенциально возможным, экспериментом.

При учёте постоянства скорости света в любой инерциальной системе отсчёта, события одновременные в одной системе, оказывались неодновременными в другой системе, двигающейся равномерно относительно первой. Этот совсем неочевидный факт, подтвердил опыт, который выполнил знаменитый физик-экспериментатор, лауреат Нобелевской премии Альберт Майкельсон (1852–1931).

По существу, принцип наблюдаемости выражает главное отличие физики от математики, где утверждения никаких опытных проверок не требуют.

Но что интересно, Эйнштейн, формулируя свой принцип, имел в виду прямые измерения. А как быть с косвенными измерениями, о которых мы говорили в предыдущей статье на эту тему?

Очень важным считал принцип прямой наблюдаемости известный физик Эрнст Мах (1838–1916). (Читателю должно быть известно число Маха.) Он даже сомневался в том, что траектория снаряда – парабола, и придумал специальный метод её «разглядеть».

Отметим, что в дальнейшем многие создатели теории относительности и квантовой механики пришли к мысли об ограниченности этого принципа. Например, нельзя наблюдать гравитационную постоянную, заряд электрона, волновую функцию в квантовой механике и т.п.

Указанные учёные, как и Эйнштейн, имели в виду применение принципа к прямым, непосредственным измерениям, хотя на это явно и не указывали. Понятно, что приложение принципа наблюдаемости к косвенным измерениям должно было бы существенно расширить область его применения.

Как должен формулироваться такой принцип?

Перед тем, как дать обобщение принципа на непрямые измерения, добавим кое-что к критике стандартной методики косвенных измерений.

Мы сомневались в выборе формулы для расчёта погрешности косвенного измерения, но заметим, что в эту формулу, к тому же, входят производные. А насколько вообще правильно применять понятие производной при расчёте погрешности? Ведь производная – это предел отношения Δу/Δх при Δх → 0, а при любом измерении х и у всегда ограничены, и указанная операция просто невыполнима.

Об этом же говорит автор солидного многотомного учебника по общей физике Д.В. Сивухин.

В томе «Механика» он пишет: «…все измерения сопровождаются погрешностями… Это обстоятельство, строго говоря, делает невозможным предельный переход Δх → 0, вводимый в математике при определении производной».

Интересно рассуждает известный советский физик Яков Борисович Зельдович. «Дело просто в том, что находить интересующие нас отношения конечных приращений трудно, поэтому и придуманы приближённые асимптотические формулы для них. Эти-то приближённые формулы математики и называют своими пределами и математическими производными. В любом реальном применении теории следует учитывать, меньше чего не следует делать приращения, чтобы результаты теории соответствовали эксперименту».

Рассуждение интересное, если не считать, что нет ответа на важный вопрос: «меньше чего не следует делать приращения»?

Ещё один, относящийся сюда вопрос: как правильно считать, чтобы «результаты теории соответствовали эксперименту»? Формула для производной, в качестве приближённой, становится особенно сомнительной, когда допустимый диапазон изменения измеряемой величины сравним с её абсолютной погрешностью.

В действительности, трудности описания эксперимента начинаются уже при использовании понятия обычной непрерывной функции. Такая функция в действительности содержит гораздо больше информации, чем необходимо для описания опыта с конечной погрешностью, ведь её значения известны в бесконечном числе точек.

Приведём пример нахождения абсолютной погрешности непрямого измерения отношения (предельным случаем которого как раз и является производная).

Пример 1. Какую максимальную длину может иметь прямоугольный участок площадью S = 20 м²?

Этот вопрос можно рассматривать, как задачу косвенного измерения одной из сторон. Как известно, площадь прямоугольника S = x×y, где x и y – длины сторон. Пусть абсолютные погрешности площади и одной из сторон соответственно ΔS = 1 м² и Δx = 1 м.

Тогда максимально возможная длина одной из сторон х_max = S / Δx = 20 м. Соответственно погрешность косвенного измерения другой стороны: Δy = S/х_max = 20 м²/20 м = 1 м, то есть Δy = Δx = 1 м.

Из оценки видно, что длина участка, которую можно измерить с указанной точностью, не произвольна, а ограничена диапазоном Δx = 1 м ≤ x ≤ 20 м = х_max.

А могут ли более длинные участки иметь площадь 20 м² при заданной точности прямых измерений? Очевидно, нет. Более длинный участок выглядит как отрезок прямой, поскольку ширину такого участка нельзя наблюдать, то есть её нельзя измерить прибором, имеющим принятую точность.

Увеличим точность в 10 раз, то есть положим: S = 20,00 м², ΔS = 0,01 м² и Δx = 0,1 м. При этом точность косвенного измерения также увеличится в 10 раз. Диапазон возможных значений длины при этом расширится до 0,1 м ≤ x ≤ 200 м.

Заметим, что в обоих случаях: Δx = Δy. Из расчетов видно, что для функции, содержащей деление (у нас – y = S / х), на делитель накладываются определённые ограничения. Посмотрим, к какому результату в указанных случаях приведёт стандартная методика с частными производными, которая в нашем случае имеет вид:

Как видно из (1), Δy зависит от длины х, чего не было в предыдущем расчёте. В случае Δх = 1 м, Δy = 1/20 + (20·1)/20² = 0,1 м ≠ Δх.

При Δх = 0,1 м, Δy = 0,01/20,0 + (20,0·0,1)/(20,0)² = 0,01 м.

Понятно, что (1) не предполагает никаких ограничений на длину х, стоящую в знаменателе формулы косвенного измерения. Кроме того, погрешность косвенного измерения Δy, рассчитанная по стандартной формуле, значительно меньше (в нашем примере – на порядок), чем аналогичная погрешность прямого измерения, и растёт с ростом этой точности.

Это обстоятельство ничем не обосновано. Более того, открывается возможность с помощью косвенного измерения, то есть с помощью формул, неограниченно улучшать точность любого измерения. Но это невозможно, хотя бы из-за квантового соотношения неопределенностей.

Пример 2. Для определения длины волны с помощью явления интерференции используют простую формулу

где λ – длина волны света, x – расстояние между соседними интерференционными полосами, y – расстояние между когерентными источниками света, z – расстояние от этих источников до экрана.

Обычно x и y измеряют микрометром с абсолютной погрешностью Δx = Δy ≥ 10 мкм, а z – миллиметровой линейкой с Δz = 1 мм. Возьмём случай реальных измерений из лабораторной практики: x = 1,2 мм, y =0,5 мм и z = 1000 мм (заметим, что здесь погрешности измерения длин z, x и y – различны).

При этом нетрудно получить λ = (1,2·0,5)/1000 = 0,6 мкм. В соответствующих опытах интерференционные полосы действительно красного цвета, что соответствует полученному значению длины волны. Но вот, все ли цифры этого числового значения 0,0006 мм достоверны?

Формула (2) похожа на зависимость из предыдущего примера. Такой же расчёт показывает, что значение переменной z здесь содержится в диапазоне: 10 мкм ≤ z ≤ 6 мм (заметим, что z = 6 мм существенно меньше реального измерения z = 1000 мм).

Что отсюда следует? То, что, по меньшей мере, две цифры полученного результата косвенного измерения недостоверны (в нашем случае λ ≈ 0,00 мм).

Из этого результата, конечно, не следует, что красному цвету не соответствует длина волны 0,6 мкм. Просто с использованными приборами получить достоверную цифру в данном опыте нельзя.

Нетрудно убедиться, что при Δx = Δy = 1 мкм граница для z возрастает до 600 мм. Для измерения x и y с требуемой степенью точности, как нетрудно видеть, необходимо пользоваться микроскопом с абсолютной погрешностью не больше 0,5 мкм, что уже меньше 0,6 мкм и даёт основание считать результат опыта в какой-то мере достоверным.

В заключение сформулируем принцип косвенной наблюдаемости, неявно использованный в наших примерах: абсолютная погрешность косвенного измерения некоторой физической величины должна быть не меньше абсолютной погрешности любого из прямых измерений аналогичной физической величины, входящей в формулу этого косвенного измерения.

Правдоподобие этого положения подтверждается тем, что возможность с помощью косвенных измерений улучшать точность (а стандартная методика это позволяет, как было видно из примеров) дало бы возможность только с помощью формул создать ряд приборов с неограниченно улучшаемой точностью.

Приведём поясняющий пример. Косвенное измерение скорости можно осуществить делением длины участка пути на соответствующий ему интервал времени. Тогда можно создать прибор, основанный на таком косвенном измерении скорости.

Это уже прибор прямого измерения, назовём его спидометр №1. Пусть сформулированное выше положение неверно, и спидометр №1 можно сделать более точным, чем допускает принцип косвенной наблюдаемости. Тогда можно построить ещё более точный спидометр №2, вычисляя уточненную с помощью спидометра №1 длину и определяя скорость уже по более точной формуле. Процесс этот можно продолжать, неограниченно улучшая точность измерения скорости.

Чтобы не создавать у читателя впечатление полной завершённости предмета вынесенного в название статьи, предложу вопрос любознательным. А как применять принцип наблюдаемости, если среди параметров формулы нет параметра, аналогичного параметрам прямых измерений? Вопрос простой, но важный. С непременным пожеланием успехов и новых открытий юным физикам.

К приведённой формулировке можно высказать следующее замечание. Косвенное измерение может иметь размерность, отличную от размерностей, входящих в формулу параметров прямых измерений. Это обстоятельство резко сужает область применения приведенных формулировок. Однако, это ограничение устраняется нормировкой всех параметров прямых измерений на их абсолютные погрешности (делим формулу (1) на соответствующие Δх). При этом для каждой переменной формула принимает вид 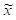= 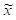_о ± 1, где 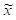= х/Δх,  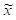_о = х_о/Δх. Множество значений параметров переходит при этом в конечное подмножество множества натуральных чисел. При этом все абсолютные погрешности как прямых, так и косвенных измерений унифицируются и становятся равными 1. Формулировка принципа косвенной наблюдаемости упрощается: достоверное значение косвенно измеряемого параметра всегда должно быть больше единицы.

Выводы. Повторим другими словами приведенную выше формулировку расширенного принципа наблюдаемости: абсолютная погрешность числового значения косвенного измерения физической величины должна быть больше, чем абсолютная погрешность любого из прямых (или достоверных, установленных, косвенных) измерений аналогичной величины, входящей в формулу этого косвенного измерения.

Таким образом, широко применяемая для анализа абсолютной погрешности косвенного измерения формула типа (3) не может быть рекомендована для обработки результатов эксперимента.

Можно высказать предположение о том, что поразительная настройка некоторых фундаментальных констант, которые получают путем косвенных измерений, является следствием неправомерной экстраполяции принципа наблюдаемости (в нашей уточнённой формулировке) за пределы его применимости.

В связи с вышеизложенным возникает ряд важных вопросов, которые требуют специального изучения. Например, насколько применим к оценке погрешностей измерения инфинитезимальный анализ, использующий непрерывные функции (большинство значений которых ненаблюдаемы) или предельный переход (выводящий значения физических величин за рамки наблюдения)?

Если существующие формулы расчёта абсолютной погрешности косвенного измерения непригодны, то каким должен быть другой, общий подход к подобным оценкам?

Каким образом, предполагая справедливым приведенный выше принцип наблюдаемости, можно улучшать точность прямого измерения, и какие физические идеи должны лежать в основе такого улучшения?

А.М. Пальти, кандидат технических наук, старший научный сотрудник по физике ВТСП