Что такое совершенство? Загадочно притягательная улыбка Джоконды? Восхитительный в своей завершенности Парфенон? Не счесть гипотез, объясняющих эти феномены. В них и гений авторов, и многое другое. Мнений много, в основном эмоциональных. Наиболее аргументированное, как и следовало ожидать, у математиков, которые языком чисел свели вековые поиски человечеством соотношения красоты и гармонии к так называемому “золотому сечению”.

пользовались соотношениями
золотого сечения
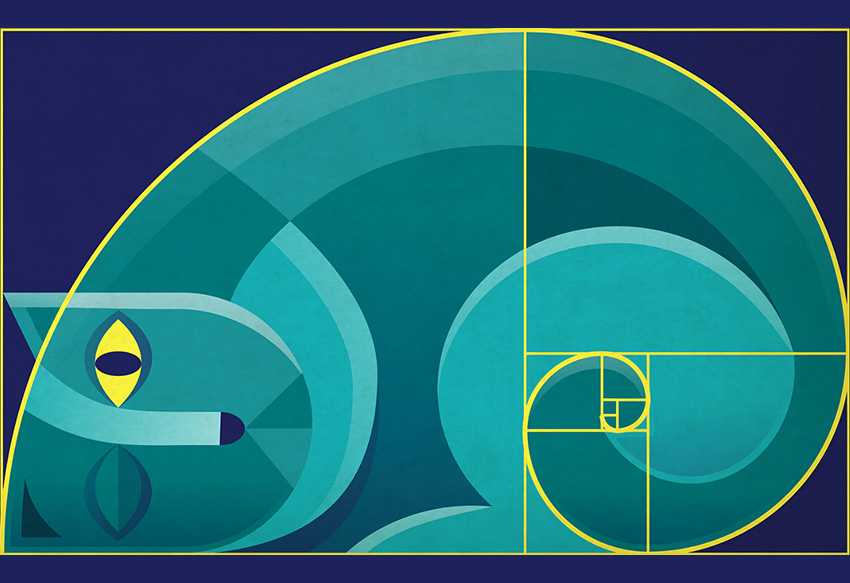
Из многих пропорций, которыми издавна пользовался человек при создании гармонических произведений, существует одна, единственная и неповторимая, обладающая уникальными свойствами. Для того чтобы целое, разделенное на две неравные части, казалось прекрасным с точки зрения формы, между меньшей и большей частями должно быть такое же отношение, как и между большей частью и целым. Или по-другому: отношение большей части к меньшей равно отношению целого к большей части. Эту пропорцию называли по-разному – “золотой”, “божественной”, “золотым сечением”, “золотым делением”, “золотым числом”.
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Принцип золотого сечения – есть высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

(1447–1517)
Сейчас невозможно достоверно установить ни человека, впервые открывшего золотую пропорцию, ни время, когда это произошло. Очевидно, её неоднократно открывали, забывали и открывали заново в разное время и в различных странах.
Многие исследователи считают первооткрывателем золотой пропорции знаменитого древнегреческого математика и философа Пифагора (VI век до н.э.). Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян.
И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
Великий древнегреческий философ Платон (V-IV век до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотой пропорции. Такая пропорция отвечает гармоническому соединению. Античные скульпторы и архитекторы широко использовали её при создании своих произведений. В этом легко убедиться при изучении шедевров древнегреческого искусства.

(1452–1519)
В дошедшей до нас античной литературе золотое деление упоминается в «Началах» Евклида (ІІІ век до н.э.). После Евклида исследованием золотого деления занимались Гипсикл (ІІ век до н.э.), Папп (ІІІ век н.э.) и др.
В Средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Секреты этого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвящённым.
В эпоху Возрождения золотая пропорция возводится в ранг главного эстетического принципа. Леонардо да Винчи именует её “Sectio aurea”, откуда и получил начало термин «золотое сечение». Великий художник использовал для композиционного построения своей знаменитой Джоконды так называемый «золотой равнобедренный треугольник», в котором отношение боковой стороны к основе равно золотому сечению.
Гениальный итальянский математик Лука Пачоли написал первую книгу о золотом сечении, назвав её «Божественной пропорцией». Книга издана в 1509 году в Венеции с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. По мнению Пачоли, Бог использовал принцип золотого сечения для создания Вселенной.
Эта идея была позже использована знаменитым астрономом Иоганном Кеплером, последняя книга которого так и называлась — «Гармония Вселенной». Ему же принадлежат такие слова: «В геометрии существует два сокровища — теорема Пифагора и золотое сечение».

на портрете Джоконды
В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». О золотом сечении почти забыли.
Вновь «открыли» золотую пропорцию в середине ХІХ ст. В 1855 г. немецкий ученый Цейзинг опубликовал свой труд «Эстетические исследования». Он абсолютизировал пропорцию золотого сечения, объявив её универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили учение о пропорциях «математической эстетикой».
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры.
Цейзинг показал, как золотое сечение выражается в отрезках прямой и в числах. Когда числа, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют знаменитую последовательность Фибоначчи. Следующая книга Цейзинга имела название «Золотое деление как основной морфологический закон в природе и искусстве».
В конце ХІХ – начале ХХ ст. появилось немало чисто формалистических теорий о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.
Систематизировать все эти знания и придать им чёткую арифметическую форму фундаментальной пропорции мироздания удалось уже только в ХХ веке. Большой вклад в эти исследования внес профессор А.П. Стахов из Винницы, который ещё в 80-х годах прошлого века обосновал базис нового учения о гармонии систем, должного стать, по его мнению, основной интегрирующей наукой XXI века.
Его книги «Введение к алгоритмической теории измерения», «Коды золотой пропорции», «Компьютерная арифметика на числах Фибоначчи и золотом сечении», «Новый тип элементарной математики и компьютерной науки на основе золотого сечения» обрели широкую известность и не остались без внимания западных производителей информационных и компьютерных технологий. Канадский университет Торонто признал автора «мыслителем XXI века».
Учёные считают, что человечество уже стоит на пороге создания новой междисциплинарной науки «о гармонии систем». Суть новой науки состоит в пересмотре с точки зрения золотого сечения всей математики, начиная с Пифагора. Это, естественно, приведет к очень интересным математическим результатам. В практическом отношении – вызовет «золотую» компьютеризацию. А поскольку «математика гармонии» существенно дополнит классическую математику, придётся пересмотреть и всю систему современного математического образования.
(1938 г.р.)
Золотое сечение – это константа всего мироздания. Оно относится к большинству, если не ко всем сферам современной науки. В том числе к биологии и ботанике. Например, ананас, кактус, сосновая шишка имеют именно «золотые» пропорции. Ощутимый прорыв в современных представлениях о природе формообразования биологических объектов сделал в начале 90-х годов ХХ ст. украинский ученый Олег Боднар, создавший новую геометрическую теорию филлотаксиса (расположения цветков).
Математика гармонии применима и к современной экономике. Довольно известны, например, работы российского ученого Харитонова об экономическом развитии российских регионов и страны в целом исходя из принципов золотого сечения.
Благодаря исследованиям американских учёных Эллиота, Пречтера и Фишера числа Фибоначчи, которые тесно связаны с золотой пропорцией, вошли в сферу бизнеса как основа оптимальных стратегий.
Советский математик Юрий Матиясевич с использованием чисел Фибоначчи решил десятую проблему Гильберта.
Российский физик-теоретик Юрий Владимиров открыл принцип золотого сечения в структуре атома.
А наиболее перспективным направлением применения новой математики будут компьютерные технологии.
Профессор А.П. Стахов, академик Академии инженерных наук Украины, один из разработчиков современной теории золотого сечения и применения чисел Фибоначчи в компьютерной технике, создал первый в мире Музей гармонии и золотого сечения.
Пропорция золотого сечения
В знаменитых «Началах» Евклид рассмотрел задачу о делении отрезка прямой в крайнем и среднем отношении, которое впоследствии Леонардо да Винчи назвал золотым сечением. Такое деление называют ещё гармоническим.

Точка Х делит отрезок АВ в крайнем и среднем отношении, если отношение большей части АХ к меньшей части ВХ равно отношению всего отрезка АВ к его большей части АХ (рис. 1).
Записанное в виде равенства отношений золотое сечение имеет вид:
АХ/ВХ=АВ/АХ.
Положим АХ=а, ВХ=b, АВ=с. Тогда а/b=с/а. С учетом того, что а+b=с, можно записать: а/b=(а+b)/а или а/b=1+b/а. Обозначим а/b=Ф, b/а=φ. Тогда приходим к системе уравнений: Ф=1+φ и Ф·φ=1.
Исключая Ф, получим квадратное уравнение: (1+φ)φ=1 или φ2 + φ – 1 = 0. Это уравнение имеет положительный корень φ = 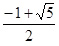 » 0,61803398…
» 0,61803398…
Тогда Ф = 1+φ = 1/φ = 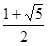 » 1,61803398…
» 1,61803398…
Здесь Φ и φ – прописная и строчная формы греческой буквы «фи». Такое обозначение принято в честь древнегреческого скульптора Фидия (V век до н.э.). Он руководил строительством храма Парфенон в Афинах. В пропорциях этого храма многократно присутствует значение числа φ.
Весьма любопытно, что эти числа можно записать в виде бесконечного радикала и бесконечной дроби:
Φ = 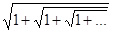 , φ =
, φ = 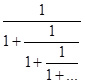
Число φ – единственное положительное число, которое превращается в обратное себе при прибавлении единицы: φ + 1 = 1/φ.
Обратим внимание на удивительные свойства золотой пропорции:
Ф2 – Ф = 1; 1/Ф2 + 1/Ф = 1; Ф + 1/Ф2 = 2; Ф2 + 1/Ф2 = 3 и т.д.
С золотой пропорцией тесно связан ряд чисел Фибоначчи 1,1,2,3,5,8,13,21,34,55,89 и т.д. В этом ряду каждое последующее число является суммой двух предыдущих чисел.
И. Кеплер установил, что последовательность отношений соседних чисел ряда Фибоначчи 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, … стремится к золотой пропорции Ф.
Числа Фибоначчи часто появляются в самых неожиданных местах, при этом неотступно сопровождая золотую пропорцию.
Золотые фигуры
(Продолжение в следующем номере)
Литература
- Васютинский Н. Золотая пропорция. – М.:Молодая гвардия, 1990.
- Азевич А. Двадцать уроков гармонии. – М.:Школа-Пресс, 1998.
- Гарднер М. Математические головоломки и развлечения. – М.:Мир, 1971.
- Пидоу Д. Геометрия и искусство. – М.: Мир, 1989.
Н.В. Шмигевский, кандидат физико-математических наук
По теме:
|
Моделирование эстетической геометрии: видео-арт и планетная система в 14 иллюстрациях |









 Основатель и издатель
Основатель и издатель Copyright © 2016–2021 Научно-популярный
Copyright © 2016–2021 Научно-популярный