Игра – это идеализированная математическая модель коллективного поведения в условиях конфликта.

В игре всегда принимает участие несколько игроков, при этом действия каждого из них влияют на последствия игры, а их интересы отличаются. В этом состоит принципиальное отличие теории игр от теории оптимизации. Везде, где только существует взаимодействие самостоятельных рациональных субъектов, возникает игра.

При помощи игровых моделей описываются модели рыночной конкуренции, войн, возникновения и распада монополий, правила использования природных ресурсов, распределения диапазонов частот между радиостанциями.

При помощи теоретико-игровых методов были получены фундаментальные результаты в эволюционной биологии. Игровые модели объясняют особенности поведения животных – такие, как агрессивность, миграция, борьба за выживание.

Теория игр – это достаточно молодая наука, ей ещё не исполнилось 80 лет. Впервые математические аспекты теории игр были изложены в книге Джона Фон Неймана и Оскара Моргенштерна «Теория игр и экономическое поведение».

В 1949 г. Джон Нэш пишет диссертацию по теории игр, а в 1994 г. он становится лауреатом Нобелевской премии по экономике, а понятие «равновесие по Нэшу» становится ключевым понятием теории игр.

О Нэше в 2002 г. был снят фильм «Beautiful mind», который демонстрировался в отечественном прокате под названием «Игры разума».

Одним из основных допущений теории игр является эгоистичность индивидов. Предполагается, что каждый из игроков стремится достигнуть максимальной выгоды для себя и безразличен к интересам других игроков.

Типичным примером такого поведения являются аукционы. Если бы все покупатели на аукционе действовали сообща, то они бы купили все необходимые вещи за начальные цены, а потом распределили бы их между собой каким-то образом. На самом же деле участники аукциона готовы платить в ходе торгов цены, большие начальных, исходя из эгоистических соображений: «Пусть эта вещь достанется именно мне, а не кому-нибудь другому».

Известным удачным примером преобразования эгоистичных мотивов индивидов в социальное благо является патентование. Если бы не было патентов, то научно-технический процесс осуществлялся бы значительно медленнее, поскольку у изобретателей не было бы материального стимула.

Патентование – это фактически игра, в которой тот, кто изобретёт и запатентует что-либо полезное раньше других, выигрывает некоторую сумму денег в виде отчислений, которые будут поступать от предпринимателей, которые используют идеи изобретателя в ходе производства.

Известные изобретатели Томас Эдисон и Никола Тесла разбогатели именно за счёт продажи патентов.

Одним из наиболее интересных направлений в теории игр является исследование так называемых коммерческих, или настольных, игр – шахмат, шашек, нард, домино, бриджа и т.д.

В настоящее время такие исследования переживают бум, и это связано как с ростом возможностей вычислительной техники, так и с развитием теории нейронных сетей и динамического программирования.

Для всех популярных игр созданы программы, которые называются боты. Такие программы в каждой ситуации могут находить оптимальный ход. Естественно, боты не могут дать пояснение, почему именно данный ход является оптимальным и научить игрока хорошо играть. Но они могут выступать в роли виртуального партнёра, имитируя игрока любого уровня – от новичка до совершенного. Появление ботов позволило развить теорию настольных игр и проанализировать ситуации, относительно которых среди профессионалов и чемпионов мира не было единого мнения.

Иногда анализ рационального поведения игроков методами теории игр приводит к парадоксальным результатам. Рассмотрим такой пример.

Пусть есть два игрока – А и В. Некто предлагает им 100 долларов за участие в простой игре. Каждый из игроков по очереди должен последовательно называть целые числа от 1 до 100 (А – нечётные, В – чётные числа). Во время своего хода игрок должен назвать следующее число или сказать «хватит». После этого игроки на двоих получат сумму, равную числу, после которого кто-то сказал «хватит», причём, игрок, сказавший это слово, получает 60 процентов суммы, другой – 40.

Проанализируем данную игру с конца. Пусть В должен сказать «100» или «хватит». Если В скажет «100», то А скажет «хватит», и в результате А получит 60, а В – 40 долларов. Выходит, что для В лучше сказать «хватит» и получить 60 процентов от 99, чем 40 процентов от 100 долларов. Но это понимает А, и ему, в свою очередь, лучше сказать «хватит», чем 99 и так далее. Таким образом, уже после того, как А скажет «3», В должен говорить «хватит». При этом сам он получит 1.80, а А получит 1.20.

Такие контрпримеры никак не опровергают важность и силу теории игр. Они лишь делают её более привлекательной и загадочной.

Повторяющиеся игры

В повторяющейся игре игроки играют в одну и ту же игру многократно. Существенную разницу между одноразовыми и повторяющимися играми удачно иллюстрирует детский анекдот.

Новый учитель математики заметил, что ученики называют одного мальчика дурачком.
– Зачем вы его обижаете? – спросил он.
– А Вы убедитесь в этом сами, – ответил один из учеников. – Он даже не понимает ценности денег. Покажите ему 5 или 10 гривен и предложите выбрать купюру.
Учитель сделал так и "дурачок" взял 5 гривен.
– Но почему ты выбрал 5? – Спросил учитель.
– Потому, что Хмельницкий мне больше нравится, чем Мазепа.
Через некоторое время учитель вызвал мальчика и спросил:
– Ты ведь в действительности весьма неглупый, и контрольные пишешь хорошо, тогда скажи честно, почему ты взял тогда 5 гривен, а не 10?
– Потому, что если я хоть раз возьму 10, то мне перестанут давать деньги!

Это, конечно, шутливый пример, но применение теории многоразовых игр помогает решить очень серьёзные проблемы. Одной из таких проблем является борьба с терроризмом и проблема освобождение заложников.

Пусть террористы захватили заложников и требуют выкуп. Что делать: уплатить выкуп или оказывать террористам сопротивление, рискуя при этом жизнью заложников?

Наилучшим исходом для захваченных заложников будет, конечно, выплата выкупа. Именно так следовало бы поступить, если это был бы единичный случай. Но на самом деле, если не чинить сопротивления, то террористы поймут, что захват заложников является выгодным бизнесом и подобные действия можно повторять регулярно. Поэтому, как это ни выглядит цинично, но властям приходится пытаться освобождать заложников силовыми методами, рискуя при этом их жизнью.

Именно этот принцип был показан в фильме «Все деньги мира» (2017 г.). Это фильм, основанный на реальных событиях, история семейства Гетти, основатель которого, мультимиллиардер Жан Пол Гетти отказался платить выкуп похитителям своего внука.

Шестнадцатилетнего юношу похищают в центре Рима и требуют выкуп в размере 17 млн долларов. Для его деда эта сумма – все равно, что простому человеку за парковку заплатить. Но он отказался, аргументируя это следующим образом: «У меня десять внуков, и жизни одного из них угрожает опасность. Но если я заплачу выкуп, то привлекательными для похищения станут все мои внуки».

Классическим примером, иллюстрирующим разницу между одноразовыми и повторяющимися играми, является игра «Мир или агрессия».

Пусть есть две страны, правительства которых решают, какую проводить политику – мирную или агрессивную. Если обе страны придерживаются мирной политики, то их затраты на вооружение равны нулю, а если агрессивную, то 1. Если же агрессию выбирает только одна страна, то она покоряет вторую и за её счет компенсирует свои затраты на вооружение и ещё получает дополнительную прибыль.

Таким образом, страна, которая вела мирную политику и не смогла себя защитить, вынуждена потратить 2 единицы. Ниже затраты обозначены через -1, прибыль – 1.

	Мир	Агрессия
Мир	(0, 0)	(-2, 1)
Агрессия	(1, -2)	(1, 1)

При этом каждый из участников переговоров говорит: «Мы будем мирными до тех пор, пока вы будете мирными. Если Вы станете агрессивными, то мы также станем агрессивными на следующем же шаге».

Действительно, неожиданная агрессивность одной из стран принесёт ей на одном шаге прибыль 1. Но она будет вынуждена потратить эту прибыль на следующем шаге на противостояние агрессивности другой страны, а на последующих шагах она будет иметь лишь дополнительные затраты.

Другой пример – наличие транспортных контролёров. В ряде случаев сумма штрафов, взимаемых контролёрами с пассажиров, оказывается меньшей, чем заработная плата самих контролёров. Но даже в этом случае содержать штат контролёров для транспортников является рациональной стратегией, поскольку само наличие контролёров стимулирует пассажиров своевременно оплачивать проезд.

Бельгийский город Антверпен известен во всём мире благодаря производству бриллиантов. По старинной традиции все соглашения между теми, кто контролирует этот бизнес, заключаются устно и вступают в силу после рукопожатия. И дело тут не только и не столько в кристальной честности и порядочности бизнесменов. Нарушив такого рода соглашение, кое-кто действительно может получить дополнительно несколько тысяч евро. Но при этом он потеряет репутацию, а, следовательно, возможность зарабатывать в сверхприбыльном бизнесе на протяжении всей жизни, а это стоит значительно дороже.

Кооперативные игры

Теория кооперативных игр изучает ситуации, в которых игроки действуют сообща, стремясь максимизировать суммарную выгоду, и временно забывают о личных интересах. Но после того, как максимальная выгода была достигнута, возникает вопрос о справедливом распределении выигрыша. При этом каждый из игроков либо группа игроков может угрожать выйти из общей группы и зарабатывать самостоятельно. Поиск справедливого распределения совместно заработанных средств является основной целью кооперативной теории игр.

Например, рассмотрим простейшую задачу о назначениях с заданной матрицей эффективностей.

		Работы
		1	2
Работники	A	6	2
	B	7	5

На первый взгляд, это – тривиальная задача. Существует два варианта назначений: А на 1, В на 2 – при этом суммарная эффективность работников равна 6+5=11, или А на 2, В на 1 – при этом суммарная эффективность равна 2+7=9. Очевидно, первый вариант лучше. Это правильный ответ с точки зрения теории оптимизации. Но заметим, что такое распределение работников по работам несправедливо.

Действительно, В получает меньше А. Вместе с тем, В лучше, чем А, поскольку его эффективность на каждой из работ выше, чем у А. Найти механизм справедливого перераспределения можно, используя математический аппарат кооперативной теории игр.

Рассмотрим данную конфликтную ситуацию. Хотя работники имеют разную квалификацию, они имеют равные права на выбор работы. Поэтому рассмотрим два случая.

Пусть в первом случае А имеет приоритет в выборе работы, тогда он выбирает первую работу и получит 6. В остётся работать на второй работе и получит 5.

Во втором случае, пусть приоритет имеет В – тогда он выберет первую работу, заработает 7, а А останется первая работа, на которой он заработает лишь 2. Таким образом, заработки А и В, усреднённые по двум случая предоставления приоритета, составляют  (6+2)/2=4 и (5+7)/2=6, всего 10. Но у А и В вместе есть возможность заработать 11. Именно так и надо поступить, а избыток денег 11-10=1 разделить пополам.

Таким образом, заработки А и В могут составлять 4.5 и 6.5 соответственно. В данном случае А работает на 1-й работе, В на второй, и А из 6 единиц своего заработка выплачивает В компенсацию в размере 1.5.

Эгоистичное поведение водителей и анархия в сетях

Пусть существует два пути добраться из пункта Start (S) в пункт End (E) – через пункт А или В, и ежедневно 4 тысячи автомобилистов выбирают один из двух путей.

Пусть дороги от S до В и от А до Е широкие и длинные и время в пути не зависит от количества автомобилей, едущих по ним, и равно 45 мин., а дороги от S до А и от В до Е короткие, но узкие, и время проезда по ним равно T/100, где T – общее число автомобилей, идущих по дороге.

Понятно, что каждый из автомобилистов исходит из эгоистических соображений – он старается минимизировать время в дороге для себя и безразличен к тому, какое время проводят в дороге другие. Таким образом, в конечном итоге в сети установится ситуация равновесия: половина водителей будет выбирать маршрут S-A-E, половина – S-B-E. При этом время каждого водителя в пути будет равен 2000/100+45=65 мин.

Пусть теперь власти решили улучшить транспортную ситуацию и построили мост между пунктами А и В. Мост оказался достаточно широким и коротким, так что время проезда по нему равно нулю.

Теперь каждый из водителей рассуждает таким образом: лучше проехать по маршруту S-A, и это займёт максимум 4000/100=40 мин. – в любом случае, это меньше, чем по маршруту S-B; потом, исходя из аналогичных соображений, не стоит выбирать маршрут A-E, лучше переехать через мост и выбрать маршрут B-E. Но так думают все водители, и если все поедут по маршруту S-A-B-E, то время в дороге для каждого составит 4000/100+4000/100=80 мин.

В очередной раз справедливой оказалась поговорка: «Хотели как лучше, а вышло, как всегда».

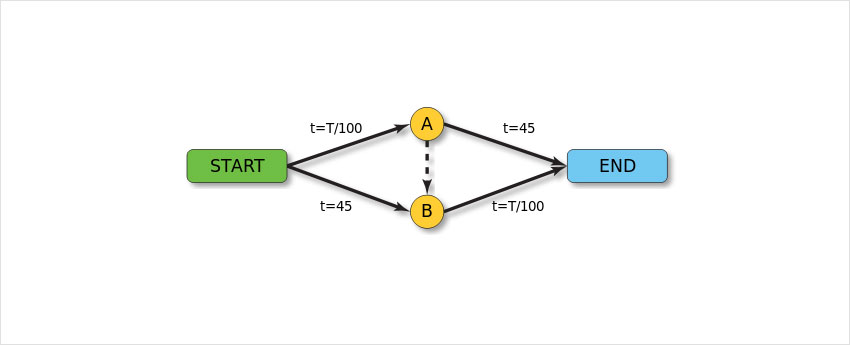
Этот на первый взгляд странный парадокс объясняется просто. Когда решается задача поиска минимума или максимума одним агентом, то, очевидно, расширение множества допустимых решений не ухудшает оптимального решения. Если же рассматривается игровая задача (т.е. ситуация, в которой есть несколько участников, каждый имеет собственные интересы и безразличен к интересам других), то это не обязательно так. Расширение возможностей может как улучшать, так и ухудшать ситуацию для каждого, и может даже ухудшить ситуацию для всех агентов сразу, как в данном примере.

Следует заметить, что железнодорожная или авиационная транспортная сеть всегда содержит в себе игровую модель, в которой в качестве игроков выступают пассажиры, а правила игры диктуются расписанием и ценами на билеты.

Каждый из пассажиров, исходя из своих потребностей и финансовых возможностей, покупает себе билет. Когда билеты становятся дефицитными, то каждый из пассажиров мыслит эгоистично: «Кому-то не хватит билетов, но пусть это буду не я, а кто-то другой». Поэтому билеты на дефицитные направления (например, летом – в курортные города) принято брать заблаговременно, даже если планы пассажира не вполне определились, и ему придётся возвращать купленные билеты.

В 2010 г. вследствие извержения вулкана в Исландии были отменены некоторые авиационные рейсы, что спровоцировало коллапс в системе авиаперевозок во всей Европе, даже по направлениям, далёким от вулкана.

Сложившаяся ситуация исследовалась методами теории игр. Дело в том, что пассажиры, рейсы которых были отменены, искали другие, комбинированные варианты (неважно, что более дорогие и менее удобные) и покупали несколько билетов с пересадками вместо одного, ухудшая ситуацию для других пассажиров. Другие пассажиры, в свою очередь, вследствие того, что их билеты были раскуплены, также искали комбинированные варианты, ухудшая ситуацию ещё больше. Сработал эффект лавины.

Ситуация оказалась бы гораздо менее критичной, если бы все перевозчики в экстремальной ситуации временно приостановили бы продажу билетов, собрали запросы всех пассажиров и нашли для каждого вариант, минимизирующий суммарные неудобства.

Забастовки транспортных работников – это тоже своеобразная игра, в которой игроками являются работники и работодатели. Очень часто такие забастовки не являются следствием тяжёлых условий работы или низкой зарплаты, а носят характер шантажа. Работники понимают, что вследствие их забастовок работодатели несут колоссальные убытки, в то время как убытки самих работников незначительны.

Отдельным классом игр являются так называемые дифференциальные игры преследования. Игроки в таких задачах делятся на преследующих и убегающих. Целью преследующего является как можно быстрее догнать убегающего, а цель убегающего противопроложна – убежать от преследующего. А если это невозможно, то нужно максимизировать время до момента, когда его поймает преследователь.

Простейший случай такой игры на однородной плоскости был рассмотрен ещё Леонардом Эйлером. Он сделал простые и понятные выводы: в каждый момент времени вектор скорости преследователя должен быть направлен на убегающего, а вектор скорости убегающего – от преследователя. Усложнение условий задачи ведёт к существенному усложнению решения. Решения подобных задач стают сложными и громоздкими и требуют значительных вычислительных ресурсов.

Тут возникает больше вопросов, чем ответов. Название «дифференциальные игры» родилось в начале исследований этого раздела теории игр в надежде на то, что траектории преследующего и убегающего можно будет описывать с использованием аппарата дифференциальных уравнений. На сегодняшний день можно сказать, что такие надежды не оправдались, но название сохранилось, как традиция.

Вместе с тем подобного рода задачи успешно решают животные, а человеку остаётся наблюдать за ними и удивляться. Даже простой таракан, спасая свою жизнь, может за долю секунды найти для себя лучшую траекторию, чем её вычислит компьютер.

Всё сказанное выше – далеко не полный перечень сфер применения теории игр, и с течением времени круг её задач и применений будет расширяться.

Безусловно, теория игр является одним из наиболее интересных разделов методов оптимизации.

Литература:

1. Дж. Д. Вильямс. Совершенный стратег, или букварь по теории стратегических игр. – Изд-во Либроком, 2009.
2. А. Шень. Игры и стратегии с точки зрения математики. – Москва: МЦНМО, 2008.
   С разрешения автора электронная версия книги свободно распространяется и доступна на сайте ftp://ftp.mccme.ru/users/shen/games.zip
3. Дж. Фон Нейман, О. Моргенштерн. Теория игр и экономическое поведение. – Изд-во «Наука», 1970.

С.И. Доценко, кандидат физико-математических наук, доцент, Институт Кибернетики имени В.М. Глушкова АН Украины