Часть 2. Via media! Держись середины

«Между тут и среди здесь»

Но всё, о чём было написано в части 1 нашей статьи, касается лишь средних двух величин. Можно ли говорить о средней нескольких величин? Интуиция в этом случае молчит. Одесское выражение, вынесенное в заголовок раздела, как нельзя лучше характеризует сложившуюся ситуацию. А что говорит математика?

Великий французский математик XIX века Огюст Коши ввёл простое определение: «Средней нескольких величин является новая величина, заключающаяся между наименьшей и наибольшей из рассматриваемых величин».¹ Однако, определение О.Коши не является конструктивным, т.е. не содержит «намёка» на то, как эти средние вычислять.

Приведенный в части 1 «балансировочный» подход не может быть использован для обобщения понятия средних при количестве исходных величин, большем двух.

В школьном курсе математики такое обобщение осуществляется формально (лишь на основании вида соответствующих формул для двух исходных величин), например:

• для средней арифметической: ;
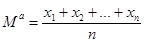• для средней геометрической: .

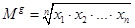Но формальный способ построения средних не является ни единственным, ни самым конструктивным. Более конструктивным является описанный в первой части подход «численного соответствия». Рассмотрим его конкретное применение.

1. Пусть f(x₁,x₂,…,x_n) = x₁+x₂+…+x_n. Будем искать такое число M^a, что f(M^a, M^a,…, M^a) = f(x₁+x₂+…+x_n), т.е. nM^a = x₁+x₂+…+x_n. Из последнего уравнения находим 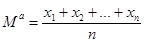, что как раз и соответствует формально введённой средней арифметической нескольких величин.

2. Если f(x₁,x₂,…,x_n) = x₁·x₂·…·x_n, то применение принципа численного соответствия приводит к средней геометрической .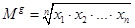

3. Применение принципа численного соответствия к функции 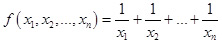приводит к средней гармонической .

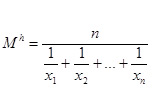Нетрудно доказать, что полученные величины M^a, M^g, M^h удовлетворяют определению Коши, т.е. являются «средними». Под впечатлением успехов применения принципа численного соответствия может показаться, что, используя этот принцип, можно получить все возможные средние.

Но это справедливо лишь для так называемых аналитических средних, т.е. средних, которые могут быть выражены в виде формулы. Однако аналитическими средними не исчерпывается всё многообразие средних. Более того, как мы увидим далее, современные представления зачастую приводят к средним именно неаналитического характера.

«Яркий представитель тёмных сил»

Рассмотрим задачу получения средней величины под ещё одним углом зрения. Будем считать, что средняя M нескольких величин x₁, x₂, …, x_n должна наилучшим образом представлять информацию обо всём множестве исходных величин (см. название данного раздела).

Иными словами, средняя M должна быть некой типичной величиной («ярким представителем») для всего множества. В силу этого число M должно быть как можно «ближе» сразу ко всем числам x₁, x₂, …, x_n.

Для отыскания M необходимо определиться, что считать мерой различия одного числа и (конечного) множества чисел. Наиболее естественно в качестве такой меры использовать сумму модулей разностей R₁ = |M – x₁| + |M – x₂| + |M – x_n|, а в качестве средней выбирать число M, при котором R₁ имеет наименьшее значение. Но математики не любят модуль — эта функция не во всех точках имеет производную, поэтому для её анализа нельзя использовать мощную «артиллерию» дифференциального исчисления.

Мы к этому вопросу вернёмся немного позже. А пока в качестве упомянутой меры различия используем лишённую этого неприятного свойства и потому любимую математиками сумму квадратов отклонений R₂ = (M – x₁)² + (M – x₂)² + (M – x_n)².

После раскрытия скобок и приведения подобных членов, мы получим квадратный трёхчлен относительно M, отыскание минимума которого не представляет труда (здесь снова на помощь может прийти средний школьник).

Проделав соответствующие выкладки, не без удивления обнаруживаем, что этот минимум достигается как раз при 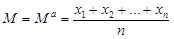! Т.е. точкой минимума функции R₂ = R₂(M) является «старая добрая» средняя арифметическая исходного множества чисел.

«САМАЯ яркая представительница тёмных сил»

И всё-таки, попробуем не пойти на поводу у этих странных математиков. Будем использовать в качестве меры различия некоторого числа M и множества чисел x₁, x₂, …, x_n величину R₁ = |M – x₁| + |M – x₂| + |M – x_n|. Ясно, что такая мера выглядит наиболее естественной. С математическими же «трудностями» её минимизации мы постараемся справиться.

Начнём мы, правда, с «пролёта», а именно рассмотрим случай n им= 2. В этом случае R₁ = |M – x₁| + |M – x₂|. Предположим, что x₂>x₁. Тогда, исходя из того, что x₁< M <x₂, имеем: R₁ = (M – x₁) + (x₂ – M) = x₂ – x₁. Таким образом, сумма расстояний внутренней точки отрезка от его концов есть постоянное число — длина этого отрезка (геометрически факт совершенно очевидный).

Т.е. в случае двух величин никакая минимизация не нужна — средней (в указанном выше смысле) оказывается любое число, большее меньшего и меньшее большего из заданных величин. Не густо! Впрочем, такое решение не противоречит определению Коши. Но очень уж оно скучное.

Однако не будем спешить сбрасывать со счёта меру R₁. В случае n > 2 она своё возьмёт. Имеет место следующий факт: меру R₁ минимизирует число M*, которое отыскивается следующим образом:

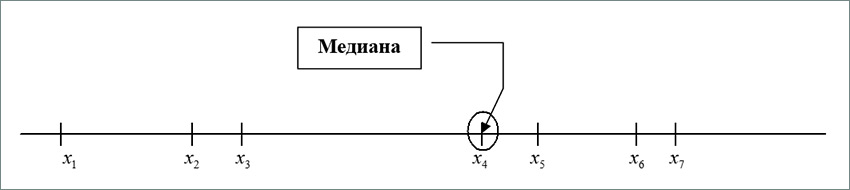
• числа x₁, x₂, …, x_n упорядочиваются по возрастанию, т.е. считаем, что x₁≤x₂≤ …≤x_n;
• если n — нечётное, то в качестве M* выбирается число x_[n/2]+1, т.е. число со средним номером;
• если n — чётное, то в качестве M* выбирается любое число из интервала [x_n/2, x_n/2+1].

Определённое таким образом число M* в общей и математической статистике называется медианой.

Как же доказать, что вышеописанная величина минимизирует меру R₁? Ведь формула для её расчёта в данном случае отсутствует! Хотя ситуация для начинающих математиков необычная, доказательство оказывается несложным.

Будем рассматривать множество порождённых последовательностью x₁, x₂, …, x_n интервалов I_k = [x_k, x_n-k+1], k = 1, …, [n/2]. Обратим внимание на то, что медиана является «самой внутренней» точкой этих интервалов, т.е. M* ϵ I_[n/2]. Для доказательства воспользуемся методом «от противного». На самом деле, если для некоторого k M* ϵ I_k и 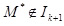, то или M* < x_k+1, или M* > x_n-k+2. Для конкретности, остановимся на случае M* < x_k+1. Тогда

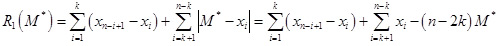
Ясно, что для 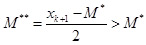получим R₁(M**) < R₁(M*), что противоречит оптимальности M*. Значит 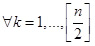имеет место включение M* ϵ I_k.

Пусть n — чётное. Тогда для всех M* ϵ I_[n/2] выполняется равенство 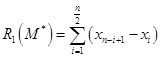, т.е. R₁ не зависит от M* (лишь бы только оно выбиралось из самого внутреннего интервала). Для избежания неоднозначности при чётном n в качестве медианы принято выбирать середину самого внутреннего интервала, т.е. .

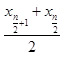Если же n — нечётное, то 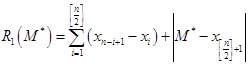, поэтому в качестве M* следует выбрать x_[n/2]+1.

Осознание экстремального свойства медианы (минимизация суммы модулей отклонений) привело к тому, что применение медианы стало «модным» в статистических исследованиях.

Дело в том, что, как мы видели выше, средняя арифметическая минимизирует сумму квадратов отклонений. Предположим, что величины регистрируются в результате проведения экспериментов или натурных испытаний, в которых возможны случайные сбои измерительного оборудования или мгновенные воздействия неконтролируемых факторов.

Тогда в нашей последовательности величин будут присутствовать так называемые выбросы — резко выделяющиеся наблюдения. Средняя арифметическая очень чувствительна к таким выбросам (в силу того, что большие отклонения от неё возводятся в квадрат).

Таким образом, наличие выбросов существенно искажает среднюю арифметическую наблюдаемых величин. При определении же медианы отклонения в квадрат не возводятся, поэтому медиана слабо чувствительна к выбросам. Это полезное свойство специалисты назвали робастностью — robust по-английски означает крепкий, устойчивый.

Заключение

Ну, а теперь главное — вовремя остановиться! Изложенных в данном «медиологическом трактате» сведений достаточно (как надеется автор) для того, чтобы читатель представил себе один из примеров зарождения абстрактного понятия, его разветвления, обобщения и углубления на протяжении колоссального периода времени — от глубокой древности до наших дней.

Отметим только, что данным «трактатом» сама тема средних величин далеко не исчерпана — скорее всего, мы остановились где-то ближе к середине.

Желающие получить больше информации по затронутому вопросу могут обратиться к «академику» Google или, что намного лучше, терпеливо подождать новых публикаций уже полюбившегося им автора данного опуса.

Б.Г. Тучинский, средний математик, кстати – доктор философии (PhD) по специальности «прикладная математика для экономики», старший научный сотрудник Института возобновляемой энергетики НАН Украины