
Вспомним два наиболее важных вопроса из предыдущей статьи. Один связан с неестественным сомкнутым (не расходится от оси) режимом течения струи, другой – с непонятным нулевым расходом (решение не учитывало вытекания в реальных условиях конечного количества жидкости из трубы).
Что касается второго вопроса, то уважаемый мною Юрий Борисович Румер нашёл решение, учитывающее ненулевой расход. Но его решение не содержало предельного случая нулевого расхода. Это довольно странное обстоятельство. Так же, как странным являлось отсутствие предела нулевой вязкости в решении Льва Давидовича Ландау.
В чём тут дело? Рассмотрим подробнее случай нулевого расхода. Что физически означает такая ситуация, и возможно ли такое вообще? Оказывается, возможно. Для этого нужно, чтобы в трубе, откуда вытекает вода, существовал обратный ток, например, вдоль её оси. Тогда вытекающая и втекающая вода суммарно дадут нулевой расход.
Но можно ли обеспечить такое течение, другими словами, существует ли соответствующее стационарное решение уравнений гидродинамики.
Полезно знать, что есть два типа течений жидкости. Это – ламинарное (плавное, устойчивое) и турбулентное (хаотичное, быстрое) течения. Решение, которое соответствовало закону Пуазёйля, издавна служило для проверки правильности самих уравнений Навье-Стокса.

(1797-1884)
Этот закон (зависимость скорости течения от расстояния до оси в трубе) соответствовал ламинарному режиму течения, которое экспериментально наблюдал ещё Готтхильф Генрих Людвиг Хаген (1839 г.) и наиболее подробно изучил Жан Луи Мари Пуазёйль (1846 г.), в честь которого и назван этот параболический закон. Но он не учитывал нелинейности уравнений, а ею, при достаточно больших скоростях жидкости, нельзя пренебрегать даже при ламинарном её течении. Как же быть в случае, учитывающем нелинейность?
С этим связана интересная история из жизни автора данной статьи, имеющая непосредственное отношение к дальнейшему повествованию. В конце третьего курса, когда пришла пора определяться с дипломом и руководителем, меня вызвал шеф отдела, где я проходил практику в Институте теплофизики Сибирского отделения АН СССР.
Он сказал мне: вам нужно выполнить курсовую работу, которая покажет, можете ли вы заниматься нашими вопросами. Поставлю перед вами задачу, а вы попробуете свои силы. Дальше шеф на доске изложил суть задачи, для решения которой нужно было найти поле скоростей в трубе с учётом отмеченной выше нелинейности. Причём вид нелинейности был достаточно произвольным.

(1799-1869)
Интересным в постановке задачи было следующее обстоятельство. Общего метода решения нелинейных уравнений пока нет, поэтому чаще всего их решают приведением к более простому линейному уравнению. Такая операция приводит к хорошему решению в некотором диапазоне изменения параметров.
В моём случае это были известные уравнения Громеки-Ламба (они вытекают из упомянутых ранее уравнений течения идеальной жидкости Эйлера). Их решением занимались многие исследователи, которые как раз и пользовались описанной выше линеаризацией.
И вот мой шеф, М.А. Гольдштик, большой любитель парадоксов, тут же на доске показал, что линеаризация приводит к нефизической бесконечности, чего ранее не заметили другие авторы.
Что это означало? А то, что решение, если оно и существует, могло быть решением непременно нелинейного уравнения. Говоря более простым языком, задача стояла найти поле скоростей в трубе, отличное от решения Пуазейля, причём при равной нулю вязкости (это чуть упрощало задачу) или доказать, что соответствующего решения не существует.
Решение нелинейного дифференциального уравнения (мы об этом упоминали) с произвольного вида нелинейностью – задача совсем непростая, честно говоря, не для студента 3-го курса, даже подающего надежды.
К этому следует добавить психологический момент. Я понимал, если не справлюсь, то, как и большинство моих товарищей по теплофизике, вынужден буду заняться экспериментом (других теоретических отделов в институте не было).
И вот два месяца изнурительной, без перерыва в размышлениях работы, – и никакого результата. А тут и майские праздники накануне летней сессии и окончательное закрепление у руководителя. И вот, когда я уже почти отчаялся и смирился со своей участью, что называется как снег на голову, пришло решение.
Надо заметить, что в это время мы слушали обязательный курс квантовой механики. При этом на практических занятиях решали задачи о поведении микрочастицы в различных потенциальных полях – прохождение частицы над ямой, проникновение ее через барьер и тому подобное. В качестве одной из таких задач мы рассматривали потенциал, получивший даже специальное название, скажем, «потенциал Лифшица».
Отметим, что нелинейность в моей задаче описывала угловую скорость воды в трубе. И вот, наверное, от безысходности, я взял этот потенциал и, аппроксимировав его полиномом 4-ой степени, подставил в своё уравнение. И о чудо, уравнение превратилось в тождество. Это было точное решение, которое описывало приосевой обратный ток в трубе. Конечно, я тут же помчался к шефу с намерением подробно рассказать о своём достижении.
Михаил Александрович не стал меня слушать и с порога сказал: давайте решение. Через пару минут расчётов на доске я удостоился ответа: да, это решение. На этом аудиенция окончилась. В течение следующего 4-го года обучения я слушал разные курсы и почти не занимался гидродинамикой, разве что посещал научный семинар нашего отдела.
Зачем так подробно об этом, казалось бы частном эпизоде моей студенческой жизни? Он скорее доказывал моё несовершенное владение математическим аппаратом, чем выявил какие-то способности. Но чем интересен описанный эпизод? Ответ простой: решение вкладывало смысл в необъяснимый ранее нулевой расход вытекающей из трубы воды. Если в трубе может существовать обратный ток, то, естественно, возможно множество ситуаций, когда суммарный расход воды равен нулю.
Обобщение Румера, учитывавшее слагаемые порядка 1/R2 (R – расстояние до устья трубы) в разложении скорости, давало решение с конечным расходом, но, что интересно, не имело смысла при нулевом расходе. Мы об этом упоминали в начале статьи. В действительности вся добавка к решению Л.Д. Ландау просто обращалась в нуль. Какие-то внутренние противоречия сидели в этой задаче.
Чтобы приблизиться, наконец, к решению, расскажу ещё об одном эпизоде из той поры. С дипломом у меня не было никаких осложнений, шеф просто дал свой старый отчёт, в котором затопленную струю ещё и вращали вокруг её оси. Данное им приближенное решение было сшито из двух частей, а от меня требовалось дать своё приближённое, но целостное решение.
Особых трудов эта работа у меня не заняла, диплом был написан. А вспоминаю здесь об этом по той причине, что решение шефа (а с ним и моё) обладало одной парадоксальной особенностью. При значениях скорости закрутки воды в струе выше некоторой величины, вблизи устья возникал приосевой обратный ток. А отчёт шефа решал важную практическую задачу повышения эффективности сгорания топлива в промышленных горелках.
Заметим, что сегодня в условиях дороговизны газа, полезно было бы сделать соответствующее приспособление на каждой кухне. Приведенный пример показывает, что мы описываем не какие-то абстрактные струи, не имеющие отношения к жизни. Струйные течения повсюду окружают нас в повседневной жизни.
Сюда можно отнести явления взаимодействия воздушного или жидкого потока с преградой. Например, обтекание автомобиля, самолета, корабля. Этим законам подчиняются ветродвигатели и яхты под парусом, разливка жидкого металла, литьё по моделям и многое другое. Теория этих явлений позволяет оптимизировать, а значит удешевить соответствующие устройства.
Если вы внимательно читали предыдущее, то вспомните рассуждение о том, как в соответствии со здравым смыслом, должна была бы течь вода из источника. Вытекающая вода должна была бы растекаться в стороны, встречая впереди лежащие слои воды. Но ведь при этом растекающаяся вода будет увлекать указанные слои, создавая описанный обратный ток.
Заметим, что реальные эксперименты с затопленными струями подтверждают приведенное качественное описание течения струи. И это даже при отсутствии закрутки потока. Почему же это не получилось у Л.Д. Ландау и даже в более точном приближении Ю.Б. Румера, в котором учитывался конечный радиус трубы?
Интересно, что при нулевом расходе, но с наличием обратного тока в трубе, возникновение приосевого обратного тока представляется ещё более естественным.
Вернёмся к главному вопросу нашего рассказа. В чём же причина несоответствующего течению струи математического решения Л.Д. Ландау.
Надо признаться, что в молодости автор был более удачлив. Вместо двух месяцев как в те студенческие времена, для ответа на вопрос, связанный с парадоксом Л.Д. Ландау потребовалось всего-то каких-нибудь 20 лет.
Конечно, не было того напряжения всех сил, как в задаче с вихрем в трубе, и занимался я совершенно другими вопросами, но не забывал о том парадоксе, который волновал меня ещё в те времена. Всё оказалось так просто и естественно, что теперь не могу даже точно вспомнить, когда пришла в голову нужная мысль.
А состояла она в том, что Л.Д. Ландау рассматривал течение во всем окружающем источник пространстве и, естественно, описывал всё одним уравнением. В действительности, если из источника вытекает вода, то эта вода отлична от той, что окружает трубу. И эти два разных взаимодействующих течения следует описывать разными, хотя и одного вида, уравнениями.
При этом следовало только учесть, что в месте соприкосновения этих течений, на границе между струей и затопленным пространством, скорости воды должны быть одинаковыми (условие непрерывности). Таким образом, следовало сшить два однотипных решения в дополняющих друг друга конических областях. Пример построения линий тока воды вблизи устья трубы, соответствующих полученному решению, приведён на рисунке.
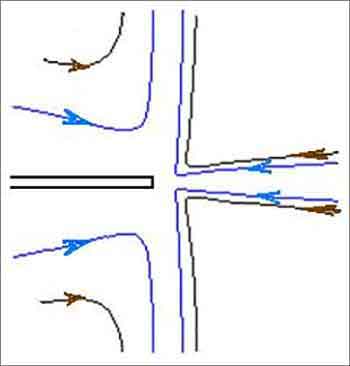
вблизи устья трубы
Такое расширение потока отвечает определенному расходу (точнее, потоку импульса) воды истекающей из источника. При этом было получено точное решение уравнений Навье-Стокса, описывающее реальное течение затопленной струи.
Конечно, на этом можно было бы поставить точку, дав заинтересовавшемуся читателю ссылку на статью в научном журнале. Но на этом история затопленного течения не закончилась.
Представьте себе стотонную металлургическую электрошлаковую печь для выплавки огромных слитков-слябов. Оборудование этой печи на заводе занимало целый цех размером в сотни квадратных метров. Такой была новейшая разработка почтенного научного института.
И вот пришла пора испытаний печи в промышленных условиях. Провели одну плавку, вторую и третью … последнюю. Почему-то вместо слябов получались блины массой в несколько тонн. Цех пришлось закрыть. Сколько средств ушло на ветер, сколько труда конструкторов, разработчиков (об учёных умолчим) – и такой результат. Это был крупный провал, о котором не писали газеты.
В чем же причина неудачи? Почему не заработала эта монументальная печь? Сегодня можно с уверенностью сказать, что причина в недооценке физической науки. Но для нашей статьи важен другой вопрос. Какое эта металлургическая проблема имеет отношение к нашим гидродинамическим изысканиям? Но об этом, как вы уже наверное догадались, отдельный рассказ и в нём описанные выше исследования играют далеко не последнюю роль.
А.М. Пальти, доцент, кафедра общей и теоретической физики Физико-математического факультета Национального технического университета «КПИ» им. И.Сикорского









 Основатель и издатель
Основатель и издатель Copyright © 2016–2021 Научно-популярный
Copyright © 2016–2021 Научно-популярный