В предыдущем номере журнала (см. №9, 2019) были рассмотрены правила игры в нарды и некоторые стратегии, повышающие шансы на выигрыш на последнем этапе игры.

Теперь рассмотрим методы вычисления суммарного количества очков, которые имеют игроки. Иногда знания этой величины (своей и соперника) является принципиальным при принятии решения как относительно следующего хода, так и удвоения ставок.

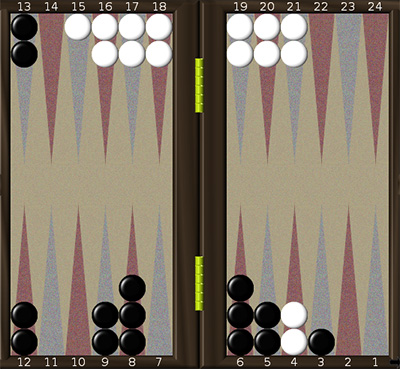
Например, рассмотрим позицию на рис. 1. В данном случае дом чёрных расположен в правом нижнем углу, дом белых – в правом верхнем. Пусть каждый из игроков ведёт собственную нумерацию полей, так что ближайшее поле в доме под номером 1, а самое отдаленное поле – номер 24.

На рис. 1 представлена нумерация чёрных. Нумерация белых связана с нумерацией чёрных простым образом: Номер поля чёрных = 25 минус номер поля белых и наоборот. Белые имеют две шашки на 1-м поле, две – на 3-м, три – на 4-м, две – на 6-м, две – на 10-м, две – на 13-м и две – на 22-м. Таким образом, суммарное количество очков для белых составляет

2·1+2·3+3·4+2·6+2·10+2·13+2·22=122.

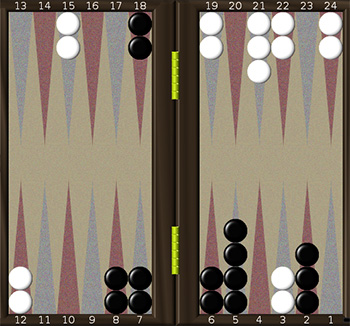
Для чёрных оно равно 3·2+4·5+2·6+2·7+2·8+2·18.

Вычисленные суммы характеризует минимальное количество очков, которое нужно выбросить игроку для того, чтобы занести все шашки в дом и выбросить их с доски, таким образом, чем меньше вычисленная сумма, тем лучше темп игрока. В данном случае чёрные имеют большое преимущество по темпу.

Вроде бы арифметика вычисления темпа для обоих игроков очень проста. Но возникает вопрос – как её сделать ещё проще, чтобы иметь возможность вычислять темп устно и быстро.

Один из профессиональных игроков в нарды, Jack Kissane, мог вычислить темп любой позиции в течение пяти секунд. Такие способности казались другим игрокам феноменальными и даже мистическими. Однажды, в 1992 году, он опубликовал статью, в которой раскрыл секрет, как ему это удаётся. Раскроем некоторые его секреты, но сначала рассмотрим два примера, не связанные с нардами.

Гаусс и формула арифметической прогрессии

О детстве выдающегося немецкого математика Карла Фридриха Гаусса (1777–1855) существует такая легенда. Школьный учитель хотел оставить учеников без присмотра на длительное время, и чтобы занять их, придумал задачу – найти сумму всех целых чисел от 1 до 100. Не успел учитель выйти из класса, как юный Гаусс ответил – 5050.

Как он это сделал? Оказывается, достаточно просто. Он к сумме чисел от 1 до 100 дописал такую ​​же, но слагаемые поставил в обратном порядке и заметил, что попарные суммы слагаемых оказываются одинаковыми, то есть 1 + 100 = 101, 2 + 99 = 101 и т.д. Всего будет 100 таких парных сумм. Таким образом, удвоенная сумма составляет 101·100=10100, и, следовательно, искомая сумма в два раза меньше и равна 5050.

Конечно, данная задача является частным случаем формулы суммы арифметической прогрессии, известной из школьного курса:

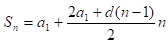 или .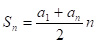

Метод мнимых нулей

Данный метод является распространённым в статистических исследованиях.

Поясним его на простом примере. Пусть путь электропоезда составляет 125 км. Пусть этот путь был разбит на 5 участков по 25 км, которые носят название «зоны». В каждой зоне есть свои остановки, а стоимость билета зависит от зоны. Пусть было продано 100 билетов, и статистика продажи приведена в следующей таблице

Зона	1	2	3	4	5	вместе
Продано билетов	11	20	34	18	17	100

Пусть надо оценить среднее расстояние, которое пассажиры проезжают в поезде.
Предположим, что пассажиры, которые взяли билеты в первую зону, в среднем проезжают 25/2=12.5 км, во вторую – 12.5+25=37.5 км, в третью – 62.5 км, в четвёртую – 87.5 км, в пятую – 112.5 км. Таким образом, среднее расстояние будет составлять

0.01· (12.5·11+37.5·12+62.5·34+87.5·18+112.5·17)=65 км.

Простые вычисления, но не совсем удобные. О том, чтобы сделать их устно, речи не идёт. Но поскольку интервалы между соседними значениями расстояния равны, можно применить метод мнимых нулей. Введём новую шкалу расстояний, состоящую из нуля и целых чисел, как показано в таблице.

Продано билетов, n_i1120341817100

Зона	1	2	3	4	5	вместе
расстояние, xi, км	12.5	37.5	62.5	87.5	112.5
мнимое расстояние, yi	-2	-1	0	1	2

Тогда мнимое среднее расстояние вычисляется по формуле .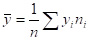

В данном случае вычисления очень простые – .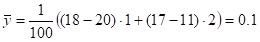

Теперь перейдём от мнимого расстояния 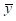 к реальному искомому значению среднего расстояния 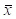. Сделать это достаточно просто.

Пусть h – ширина интервала (или, другими словами, разница между соседними значениями, x_i, x*– значения x_i, напротив которых стоит нулевое значение, (или воображаемый нуль). В данном случае h=25 км, x*=62.5 км.
Тогда 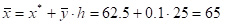км. Такие вычисления уже легко делать даже устно.

Вернёмся к нардам и рассмотрим некоторые технические приёмы вычислений.

1) «Зеркало». Пара шашек, которые стоят на доске одна напротив другой, всегда дают 25 очков. Действительно, такая пара шашек может занимать 1-ю и 24-ю позиции, или 2-ю и 23-ю и т.д., или 12-ю и 13-ю. Но в любом случае сумма двух чисел равна 25. Очень похоже на приём, применённый юным Гауссом.

2) Симметричная фигура (или симметричный кластер). Если группа шашек образует симметричную фигуру, то сумма их позиций равна произведению количества шашек на номер позиции, являющейся центром симметрии.

3) Разорванный кластер. Иногда в симметричной геометрической фигуре могут быть «разрывы». Надо мысленно ликвидировать разрыв, «склеить» фигуру и вычислить соответствующее количество очков. Затем надо вычислить «поправку», то есть учесть, какое количество шашек на какое количество позиций вперёд или назад было сдвинуто с целью устранения разрыва.

4) Мнимое смещение шашек. Конечно, не все позиции такие «красивые», что их можно разбить на зеркала и симметричные кластеры. Но они становятся таковыми, если мысленно сдвинуть вперёд или назад некоторые шашки.

5) Мнимое смещение квадрантов. Напомним, что игровое поле разбито на четыре квадранта. Первым квадрантом игрока называется его дом (поля 1-6), вторым – поля 7-12, третьим – 13-18, и четвёртым – 19-24.
Пусть несколько шашек находятся во 2-м, 3-м или 4-м квадранте. Мысленно передвинем эти шашки в первый квадрант. Теперь уже множители принимают значения от 1 до 6, и вычислить соответствующую сумму значительно проще. К вычисленной сумме надо добавить
(количество сдвинутых шашек) × (номер квадранта минус 1).

6) Мнимый центр тяжести. Пусть группа шашек не является симметричной, но шашки сконцентрированы вокруг некоторой позиции. Умножим количество шашек на номер позиции условного центра масс и для каждой шашки из группы вычислим поправку, равную её отклонению относительно выбранного центра. Поправку берём со знаком «+», если отклонение имеет место в сторону «дома», и «-», если в сторону «домой».

7) «Закрытая доска». В коротких нардах каждый из игроков стремится закрыть каждое из своих полей в доме двумя или больше шашками. Если в доме каждое из 6 полей закрытое двумя шашками, то это даёт в сумме (1 + 2 + 3 + 4 + 5 + 6)×2 = 42 очка.

Может оказаться такая ситуация, что к одной или нескольким шашкам невозможно применить ни один из указанных приёмов. Тогда просто надо добавить номера их позиций к общей сумме.

Разберём применение всех приёмов на примерах.

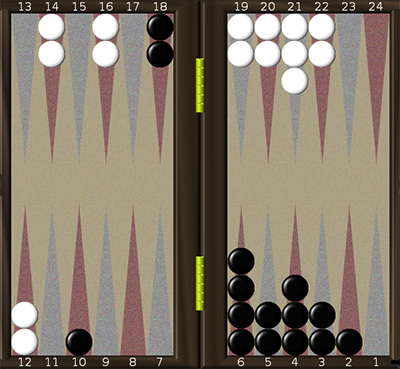
На рис. 2А. идеальная для подсчётов ситуация. Чёрные имеют симметричную фигуру на позициях с 5 по 9 (10 шашек, центр – 7, следовательно, 10×7 = 70), две зеркальные пары 12-13 (2×25 = 50) и одну отдельную шашку на 3 позиции, вместе 70 + 50 + 3 = 123.

Белые имеют в «зеркале» две пары на позициях 4 и 21 (что даёт 50), плюс блок из 10 шашек на позициях с 5 по 9 (центр – 7, следовательно, 10 × 7 = 70) плюс отдельную шашку на 10-й позиции. Итого: 50 + 70 + 10 = 130.
Ситуация на рис. 2Б не так красива, как на 2А, но её можно легко скорректировать путём мнимых смещений.

Чёрные – передвинем две шашки с 6 на 7 (поправка – -2) и одну шашку с 4 на 2 (поправка – 2). Следовательно, суммарная поправка равна нулю. Но в результате мы получили блок из 10 шашек на позициях 2-6 (центр – 4), что даёт слагаемое 40, две пары в зеркале 7-18 (слагаемое – 50) и отдельную шашку на 10-й позиции, вместе – 100.

У белых передвинем одну шашку с 4 на 5 (поправка –1), две шашки с 9 на 7, чтобы «приклеить» их в блок (поправка – +4) и две шашки с 11 на 12 (поправка – 2). Следовательно, суммарная поправка равна +1. Но в результате получаем симметричный блок с 11 шашек, центр – 5, следовательно, 11×5 = 55, две пары в зеркале (50). Итого: 50 + 55 + 1 = 106.

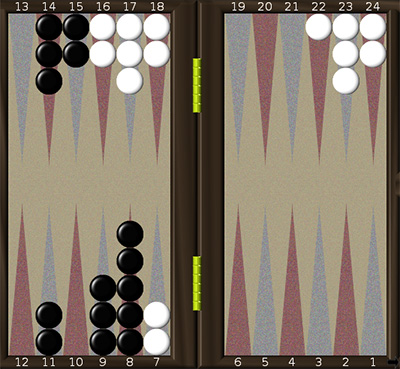
Рассмотрим позицию 3А. Даже без подсчётов очевидно сильное отставание чёрных. Для чёрных отдельно рассмотрим группы, стоящие во втором и третьем квадрантах. В третьем квадранте есть 3 шашки на 14 и две на 15. Для этой группы можно принять условный центр тяжести 14 или 15, тогда соответственно имеем: 5×14 + 2 = 72 или 5×15 - 3 = 72.

Можно мысленно переместить эти шашки в первый квадрант. Для перемещения понадобится 5×12 = 60 очков, а в первом квадранте сумма будет простой: 2×3 + 3×2 = 12, следовательно, 60 + 12 = 72. Вычислим сумму во втором квадранте. Можно передвинуть две шашки с 11 на 10 (поправка – 2) и 3 шашки с 8 на 9 (поправка – -3), в результате получим симметричную фигуру из 10 шашек на 9-й позиции.

Итак, 10×9 + (поправка минус 1) = 89. Можно мысленно передвинуть всю группу на 7 позиций вперёд и получить ситуацию 3б, для которой непосредственно вычисляем: 5 + 3×2 + 2×4 = 19.
Итак, 70 + 19 = 89. В любом случае окончательно имеем: 72 + 89 = 161.

Вычислим сумму для белых. Есть две пары в зеркале (50). 5 шашек, стоящих на позициях 8 и 9, можно передвинуть на 4 позиции вперёд (5×4 = 20), в результате имеем симметричную фигуру, изображённую на 3б. Для неё 3×11 = 33. Итак, 50 + 20 + 33 = 103.

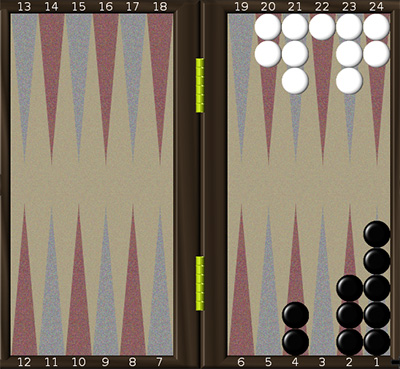
Рассмотрим пример 4А.

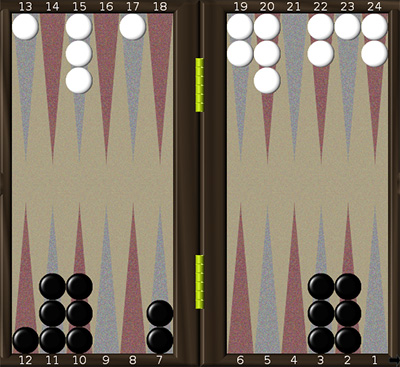
Для чёрных:
1 способ – разорванный кластер. Передвинем 2 шашки с 7 на 4 (поправка – 2×3 = 6) и 6 шашек с 10 и 11 на 5 и 6 соответственно. Следовательно, происходит смещение 6 шашек на 5 полей, 5×6 = 30. В результате получаем симметричную фигуру из 14 шашек с центром в 4, следовательно, 14×4 = 56. Ещё осталась одна шашка в позиции 12. Итак, вместе 6 + 30 + 56 + 12 = 104.

2 способ. Вычислим отдельно суммы для дома и 2-го квадранта. Для дома: (2 + 3)×3 = 15. Во 2-м квадранте находится 9 шашек. Выберем центром симметрии 10-е поле. Тогда 9×10 = 90. Поправка равна 3 + 2 - 2×3 =  -1. Итого: 15 + 90 - 1 = 104.

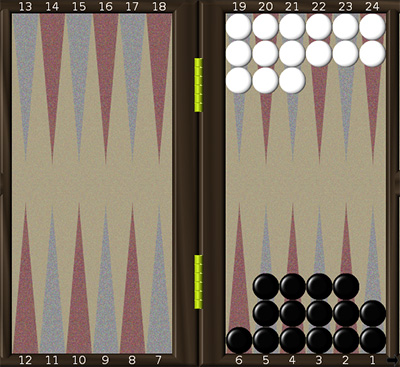
3 способ. Передвинем 9 шашек со 2-го квадранта в дом (поправка – 9×6 = 54), в результате получим позицию 4б. Эту позицию можно вычислить разными способами. Можно заметить, что это 10 шашек с центром в 3 и 5 – с центром в 4, следовательно, 10×3 + 5×4 = 50, или передвинуть одну шашку с 5 на 6 (поправка – 1), тогда просуммируем: поправка (-1) + закрытая доска (42) + 3 × 3 = 50. Можно разбить позицию на симметричную фигуру из 14 шашек с центром между 3 и 4 и одной шашкой на 1, следовательно, вместе: 14·(3+4)/2+1=50. Итого: 54+50=104.

Для белых:

1 способ. Передвинем одну шашку с 6 на 4.

Будем иметь сразу три симметричные фигуры по 5 шашек каждая, с центрами в позициях 2, 5 и 10. Следовательно, будем иметь

2×5 + 5×5 + 10×5 + (поправка 2) = 87.

2 способ. Передвинем 5 шашек со 2-го (для белых) квадранта (на рисунке 4а эти поля пронумерованы с 13 по 18) в дом (поправка 5×6 = 30), в результате получим позицию 4б). Для неё имеем (закрытая доска = 42) + 3×5 = 57, следовательно, вместе: 30 + 57 = 87.

Приём без названия. Данный приём не имеет названия, но является фактическим применением метода мнимых нулей к нардам. Его можно применять в любой ситуации. Лучше всего метод работает, когда часть шашек уже занесена в дом, остальные шашки на подходе к дому, и ещё не выброшено ни шашки.

Разобьём условно доску на зоны по три поля в зоне. Поля 1-3 назовём минус первой зоной, 4-6 – нулевой, и т.д., 22-24 – шестой. Вычислим мнимую сумму как сумму произведений номеров зон на количество шашек, что есть в каждой зоне. Если часть шашек находится в нулевой зоне, а остальные – недалеко от неё, то это можно сделать быстро. От мнимой суммы перейдем к «реальной» искомой сумме по формуле

Сумма = 3×(Мнимая сумма) + 5×(Количество шашек) + поправка.

С первым слагаемым всё понятно – это только вычисленная мнимая сумма. Если ещё не выброшено ни шашки, то второе слагаемое равно 5×15 = 75.
Поправка также исчисляется просто. Каждая зона состоит из трёх полей – среднего, ближнего и дальнего (к дому). Например, первая зона состоит из полей 7, 8 и 9. Поле 8 будет средним, 7 – ближним, 9 – дальним, и т.д. Поправка равна количеству шашек, стоящих на дальних полях, минус количество шашек, стоящих на ближних. Шашки, стоящие на средних полях, дают нулевой вклад в поправку. Поправку можно считать для каждой зоны отдельно и постепенно добавлять полученные числа или сначала по всем зонам определять положительную, а затем – отрицательную части, кому как нравится.

Вычислим суммы на примере 4а. приведенным способом. Результаты расчётов представим в таблице.

Зоны	-1	0	1	2	Мнимые суммы
Шашки чёрных	6	0	2	7	10
Поправки чёрных	+3	0	-2	-2	-1
Шашки белых	5	5	1	4	4
Поправки белых	0	+2	0	-2	0

Перейдем к реальным суммам.
Для чёрных: 3×10 + 75 - 1 = 104, для белых: 3×4 + 75 + 0 = 87.

Возникает вопрос – какие из указанных приёмов в каких ситуациях следует применять. Единого ответа нет. Здесь надо уметь видеть и догадываться – это вопрос тренировки и опыта.

Можно вспомнить афоризм Леонардо да Винчи «Существует три типа людей. Те, кто видят сами, те, кто видит, когда им показывают, и те, кто не видит».

Если читатель внимательно разобрал приведенные примеры, то его уже можно отнести ко второму типу. Автор желает читателям успешно освоить все приёмы и перейти к первому типу.

С.И. Доценко, кандидат физико-математических наук, доцент факультета информационных технологий КНУ имени Тараса Шевченко

По теме:

Игра в нарды и классическая формула вероятности

Что такое математическая теория игр

Задача коммивояжера – научимся решать её на компьютере