
Про двох великих швейцарських математиків – Якоба та Йоганна Бернуллі
...Суперечка між двома вченими про те, хто першим вирішив те чи інше завдання або довів нову теорему, хто глибше дістався суті проблеми і дав їй правильну оцінку, одним словом – хто розумніший, освіченіший, кмітливіший – дедалі розпалювалася…
Вона починалася з легких, ледь помітних «шпильок», але незабаром набула їдкого сарказму, перетворилася на обмін насмішками, а згодом і зовсім переросла у грубу взаємну хулу.
Жорстку і тривалу словесну війну не могли зупинити ані доводи розуму та почуття гідності сперечальників, ані вмовляння друзів, ані навіть висловлювання інших авторитетних та відомих учених.

(1654-1705)

(1667-1748)
Пристрасті настільки загострилися, що журнали відмовлялися друкувати наукове листування ворогуючих учених, одного з яких звали Якоб Бернуллі, а іншого – Йоганн Бернуллі. Це були не просто люди з однаковим прізвищем – Бернуллі були рідними братами, членами добропорядної протестантської родини, що займала високе положення.
Старший з братів – Якоб – був філософом, богословом і проповідником; молодший – Йоганн – магістром мистецтв і доктором медицини. Кожен із братів, переступивши християнські заповіді (обидва були людьми однієї віри і людьми глибоко віруючими), намагався затвердити свою перевагу над іншим.
І ніякі почуття жалю і каяття, ніяка любов до ближнього не могли втримати їх від бажання принизити один одного.
Істинним, глибинним захопленням обох братів була математика, яка спочатку зблизила їх, а потім зробила непримиренними суперниками і навіть ворогами, що і прискорило смерть старшого.
Ця непримиренна боротьба, що тривала протягом багатьох років, з повною підставою дозволяє назвати розповідь про двох геніальних математиків Бернуллі за аналогією з романом відомого письменника Уїлсона Мітчела, в якому змальовано ворожнечу двох братів-винахідників телебачення. Але та ворожнеча – літературна вигадка, а в нашому випадку все відбувалося в реальному житті.
Напрошується й інше, більш «сильне» порівняння братів Бернуллі з іншими рідними братами – біблійними героями Каїном і Авелем, перший з яких із заздрості вбив свого молодшого брата.
Хто ж такі були брати Бернуллі, які зненавиділи один одного, ставши посміховиськом для вченого співтовариства в кінці XVII століття?
Пращури братів разом з тисячами інших голландців залишили батьківщину внаслідок жорстоких переслідувань релігійного характеру з боку іспанського диктатора Альби, що правив Голландією під час буржуазної революції XVI століття.
Після довгих мандрівок вигнанці влаштувалися в швейцарському місті Базелі, прийнявши тамошнє громадянство і зайнявши чільне становище в суспільстві. Тут, у Базелі, в 1654 р. на світ з’явився спочатку Якоб, а через 13 років Йоганн.
Обидва брати отримали прекрасну освіту. Старший з чотирьох братів – Якоб – вивчав богослов’я та філософію в Базельському університеті, а по його закінченні читав проповіді та мав намір стати протестантським священиком.
Якоб опікав своїх братів, але особливою увагою користувався наймолодший з них – Йоганн – надзвичайно обдарований юнак, який легко оволодівав найрізноманітнішими знаннями. Йоганн, за прикладом старшого брата, також закінчив Базельський університет, отримавши спочатку ступінь магістра наук, а потім захистивши докторську дисертацію з медицини на тему «Про рух м’язів». Це був перший досвід об’єднання медицини з математикою.
Читання проповідей Якоб поєднував з глибоким вивченням математики. Поява великої комети в 1680 р. стала поштовхом для дослідження ним теорії руху небесних тіл та опублікування першої математичної роботи.
Своє захоплення математикою Якоб зумів прищепити Йоганну. З часом учитель та учень зрівнялися в знаннях і обидва стали успішно розвивати нові ідеї в математиці.
Особливе враження на братів справила стаття Лейбніца «Новий метод для максимумів і мінімумів ....», в якій вперше викладалися основи нескінченно малих величин.
Між братами Бернуллі і Лейбніцем встановилося регулярне листування. Постійний обмін новими результатами і обговорення різних математичних проблем цим тріумвіратом багато в чому сприяли становленню та розвитку диференціального й інтегрального обчислення.
Математичні заслуги братів Бернуллі були гідно оцінені сучасниками. Так, у 1699 р., коли Якобу виповнилося 45 років, а Йоганну 32 роки, вони обидва, разом з Ньютоном, Лейбніцем і ще чотирма знаменитими вченими, були обрані іноземними членами Паризької Академії Наук, таким чином набувши вищого наукового визнання.
А тепер звернемося до двох задач, вирішених братами Бернуллі. У 1696 р. у науковому журналі Йоганн опублікував наступне повідомлення «Нова задача, до вирішення якої запрошуються математики». Наведемо зміст названої замітки.
«У вертикальній площині дано дві точки А і В (рис.2). Визначити шлях АМВ, спускаючись яким під впливом власної ваги, тіло М, почавши рухатися з точки А, дійде до іншої точки В за найкоротший час. Для того, щоб зацікавити любителів подібних завдань і заохотити їх до розв’язання, доводжу до їх відома, що це завдання не зводиться до порожньої розумової спекуляції, позбавленої практичного значення, як це може комусь здатися. Насправді воно має дуже велику практичну вагу не тільки для механіки, але й для інших дисциплін, що може всім здатися неправдоподібним.
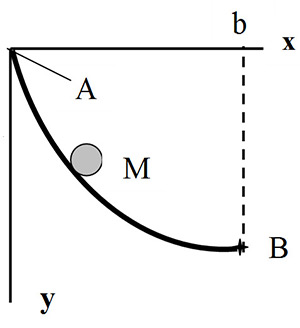
Між іншим (вказую на це з метою попередити можливе неправільне судження), хоча пряма АВ і є найкоротшою лінією між крайніми точками А і В, проте тіло проходить її НЕ за найкоротший час, й існує крива АМВ, добре відома геометрії. Я назву цю лінію, якщо по закінченню поточного року ніхто інший її не назве. Йоганн Бернуллі».
Сутність задачі, сформульованої Йоганном Бернуллі, пояснює рис.1. Зауважимо, що з нею впоралися тільки великі математики XVII-XVIII століть: Лейбніц, Ньютон, Лопіталь, сам Йоганн Бернуллі та його брат Якоб.
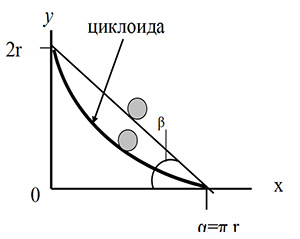
Таким чином, рішення задачі Йоганна Бернуллі зводиться до знаходження функції y (x), графік якої, що з’єднує точки А і В, є кривою найскорішого спуску, що зветься брахістохроною (Рис.1). Відкриємо секрет: в розглянутій задачі брахістохроною є циклоїда, тобто крива, яку описує точка кола, що котиться без ковзання по прямій.
Рівняння циклоїди описується двома залежністями в прямокутній системі координат:
|
|
(1) |
де r – радіус кола, за допомогою якого формується циклоїда; t – параметр, пов’язаний з кутом повороту кола.
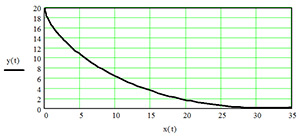
Розглянемо приклад: падіння тіла з висоти h = 2r з координатами точки старту А (0, 2r) і точки приземлення В (r, 0). Для даного випадку траєкторія падіння тіла по циклоїді при h = 20 м показана на рис. 3, а, час падіння тіла складе:
|
|
(2) |
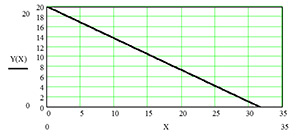
де g = 9,81 м /с2 прискорення сили тяжіння. За тих самих вихідних даних по прямій похилій лінії (рис.4, б) час падіння тіла складе:
|
|
(3) |
тобто у 1,185 разів довше. Згідно (2) при висоті h = 2r = 20 м час падіння по циклоїді складе ТЦ = 3,172 с, а по похилій прямій згідно (3) ТПР = 3,76 с.
Зауважимо, у вказаних розрахунках сила тертя, що гальмує рух, не враховується. Розглянута нами задача, сформульована Йоганном Бернуллі, стала відправною точкою для формування нового великого напряму у вищій математиці – варіаційного обчислення, присвяченого відшуканню екстремальних (максимальних і мінімальних) значень функціоналу – закону, згідно з яким кожній з функцій певного класу ставиться у відповідність число.
Відмітимо, що якщо числам ставляться у відповідність числа, то задана функція, наприклад, y(x). Якщо функціям ставляться у відповідність числа, то заданий функціонал.
За допомогою методів варіаційного обчислення вирішуються вельми важливі завдання технічного характеру: з мінімізації палива, що витрачається двигунами; оптимального швидкісного режиму руху автомобіля або поїзда; точного наведення на ціль ракети за мінімальний час і ряд інших проблем.
Пояснимо сказане. Нехай, наприклад, автомобіль повинен проїхати з пункту А в пункт В. Слід визначити графік зміни швидкості автомобіля на заданій трасі, при якому буде витрачена мінімальна кількість пального.
Інший приклад з військової галузі. Розраховується траєкторія руху ракети для враження за мінімальний час повітряної цілі, що переміщується.
Ось так маленька і здавалося б далека від практики математична задача стала тим зерном, з якого виріс великий науковий напрям прикладного характеру, яким є варіаційне числення.
А тепер звернемося до задачі, розглянутої іншим братом – Якобом Бернуллі. Є такі числа і функції в математиці, які викликають почуття подиву і захоплення у вчених. Такою залежністю для Якоба Бернуллі стала логарифмічна спіраль.
Ось що він писав з цього приводу в одній зі статей: «..І оскільки внаслідок таких чудових і незвичайних властивостей ця дивна спіраль стала настільки мені люб’язна, що я ледве міг насититися її спогляданням, я подумав, що не буде безглуздістю застосувати її для символічного представлення різних предметів.
.... Вона могла б бути символом або мужності і стійкості у скорботах, або навіть символом нашої плоті, яка воскресає тією ж самою після різних змін і, нарешті, смерті; так що, якщо б досі було у звичаї наслідувати Архімеду, то я охоче повелів би викарбувати на моїй могилі спіраль з епіграфом «Змінившись, воскресаю такою ж».
Остання фраза на латині виглядає так: «Eadem mutate resurgo».
Ось так: не більше і не менше – логарифмічна спіраль є символом нашого життя, шо вічно відроджується і в чомусь повторюється – його вмирання і воскресіння.
Воля Якоба Бернуллі була виконана: на нижній частині пам’ятної дошки, що висить у Базельському соборі, де похований великий математик, зображена спіраль, правда, не логарифмічна.
А тепер розберемося у властивостях логарифмічною спіралі – пласкої трансцендентної кривої, рівняння якої в полярних координатах має вигляд
|
|
(4) |
Формула (4) легко перетворюється у вигляд
|
|
(5) |
що і дозволяє називати спіраль логарифмічною.
При k>0 і Θ → +∞ логарифмічна спіраль розгортається за ходою годинникової стрілки, при Θ → –∞ – та ж спіраль закручується проти ходи годинникової стрілки до своєї асимптотичної точки 0. При k <0 має місце зворотна картина.
Два приклади розрахунку графіків для випадку Θ → +∞. 1) при k = 0,2; α = 3,985; 2) при k = 0,2; α = 0,2 наведені на рис.5.

Особливість усіх подібних графіків полягає в тому, що вони перетинають усі промені, що виходять з точки 0 під одним і тим самим кутом α = arkсtg (k), де k – коефіцієнт у функції (4). При k = 0 кут α = π/2 і графік спіралі перероджується в коло з радіусом ρ =a . Довжина будь-якої дуги логарифмічної спіралі
|
|
(6) |
Наприклад, згідно (6) при k = 0,2 і кутах Θ1 = 0,5π, Θ2 = π довжина спіралі L = 10,268.
Ще одна чудова властивість логарифмічної спіралі полягає в тому, що за певних перетворень вона повертається до первісного вигляду. Саме ця властивість логарифмічної спіралі викликала у Якоба Бернуллі такий захоплений відгук.
Не беремося відповісти на питання, в чому полягала причина непримиренної боротьби двох братів. Важливо інше – вони обидва були геніальними математиками, які стояли більше трьохсот років тому разом з Ньютоном і Лейбніцем біля джерел зародження диференціального й інтегрального числення.
Обидва брати стали засновниками великої династії швейцарських учених, які зробили цінний внесок у різні галузі науки і культури. Протягом понад 250 років у Базельському університеті завжди були професори Бернуллі, більше 100 років учені з ім’ям Бернуллі очолювали кафедру математики в цьому університеті, багато з них були членами Академії Наук у різних країнах.
Серед нащадків Бернуллі особливо слід виділити Даніїла Бернуллі – сина Йоганна, який працював у Петербурзькій Академії Наук та заклав основи науки «Гідродинаміка».
На закінчення наведемо слова Вольтера на смерть Йоганна Бернуллі: «Його розум бачив істину. Його серце пізнало справедливість. Він – гордість Швейцарії та всього людства». З повною підставою ті ж піднесені слова можна віднести і до Якоба Бернуллі.
Доповнення.
- Візьміть сталеву кульку і спустіть її по довгій дошці. Заміряйте за секундоміром час падіння кульки і порівняйте його з часом, розрахованим за формулою (3).
- Побудуйте графік логарифмічної спіралі при вихідних даних, відмінних від прикладу, наведеного на рис. 4.
В.І. Каганов, доктор технічних наук, професор





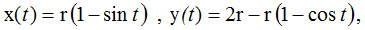
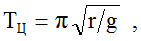
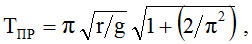
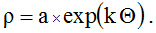
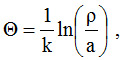
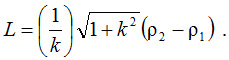











 Засновник та видавець
Засновник та видавець