Теорія ймовірностей – це застосування
математики до здорового глузду

(1749–1827)
Початок розвитку теорії ймовірностей (стохастики) відносять до XVII століття і пов’язують із комбінаторними задачами в азартних іграх. Золоті правила гри – закономірності, яким підпорядковуються випадкові події в процесі гри, – були відомі ще з давніх часів.
Хоча сьогодні теорія ймовірностей має стільки ж спільного з азартними іграми, як, наприклад, геометрія – з вимірами площ при землемірних роботах, предметом її вивчення залишаються закономірності випадкового.
Нині стохастика, подібно до інших розділів математики, – досить строга наука, що розвивається. Вона може пояснити велику кількість наукових фактів і результатів різних експериментів. Методи теорії ймовірностей відіграють особливо важливу роль у фізиці, економіці, соціології, військовій справі та багатьох інших науках.
Відомо, що завданням науки є створення системи понять про явища дійсності, а також встановлення і дослідження закономірностей, яким підпорядковуються ці реальні явища. Їх вивчення часто зумовлює потребу проводити певні експерименти і спостерігати за їх наслідками. Такі експерименти називають також дослідами або випробуваннями. Результати (наслідки) випробувань називають подіями.
На результати випробувань впливає багато різноманітних чинників, що взаємодіють між собою. Будь-яке конкретне поєднання цих чинників називають ситуацією, або сукупністю умов, або комплексом умов. Кожна ситуація створює передумови появи однієї чи декількох відповідних подій.
Наприклад, якщо комплекс умов складає: атмосферний тиск 760 мм і температура за Цельсієм, то подією буде перетворення води в пару (позначимо цю подію через А). Змінивши комплекс умов (тобто, змінивши або тиск, або температуру), подію А можна й не отримати. Цього разу може відбутися подія (вода буде в рідкому стані) або подія (вода буде в твердому стані).
Отже, кожну подію можна розглядати як результат реалізації відповідного комплексу умов. Надалі, кажучи про деяку подію, ми будемо вважати, що комплекс умов або відповідна ситуація вже зафіксована, і на цьому не будемо наголошувати.
У комплекс умов, який породжує певну подію А, включають лише основні, найбільш впливові складові. Врахувати всі фактори, що породжують подію А, практично неможливо. Тому в багатьох випадках на появу події А впливають випадкові фактори. Ці фактори можуть зумовити випадковість події.
Наприклад, метеорологічні явища зазнають впливу багатьох невизначених факторів. І ми не можемо врахувати всі сили, які діють, скажімо, на хмари. Динаміка хмар підлягає випадковим законам.
Також не можна отримати повну інформацію про всі сили, які діють у суспільстві. Суспільний розвиток – результат сумісної дії багатьох випадкових факторів. Це ж можна сказати й про поведінку окремої людини, про формування її психологічного стану.
Більшість математичних методів, які застосовують в різних галузях природознавства, техніки, економіки, гуманітарних науках спираються на уявлення про наявність випадковості в цих галузях.
Випадковість – це не вигадана математична абстракція, вона, безумовно, існує в реальному світі. Це означає, що іноді ми не в змозі отримати повну інформацію про явища не лише через наші невміння, нездатність, неточність приладів, але й об’єктивно: так влаштована природа.
У фізиці добре відомий принцип невизначеності Гейзенберга (1927 рік), згідно з яким неможливо одночасно точно визначити деякі величини, наприклад, імпульс і координату мікрочастинки. Це випливає з природи самих мікрочастинок (корпускулярно-хвильовий дуалізм), а не відбиває недоліки методу і принципів вимірювання. Справжній стан частинки можна описати тільки ймовірністю, пов’язаною з хвильовою функцією.
Сучасні наукові дослідження переконують у тому, що на квантово-механічному рівні майже всі фундаментальні закони природи мають імовірнісний характер. Такий висновок, певною мірою, є справедливим і для багатьох явищ техніки, економіки, природознавства, гуманітарних наук.
На описовому рівні випадкова подія та пов’язані з нею поняття означаються наступним чином.
Подію називають випадковою подією (або стохастичною подією), якщо при реалізації певного комплексу умов вона може відбутися або не відбутися.
Експерименти, наслідками яких є випадкові події, називають випадковими експериментами (або стохастичними експериментами).
Отже, результат випадкового експерименту не можна передбачити заздалегідь. Неможливість однозначно передбачити результат відрізняє випадковий експеримент (явище) від детермінованого.
Слово “стохастичний” походить від грецького слова здогадка. Вживається у значенні – випадковий, ймовірний.
Приклади випадкових подій: народження хлопчика в сім’ї; вступ юнака до вищого навчального закладу; банкрутство фірми в умовах кризи тощо.
Не всі випадкові події підлягають вивченню засобами теорії ймовірностей. Випадкові події, що вивчаються в теорії ймовірностей, мають дві характерні особливості.
По-перше, всі вони відбуваються в масових явищах, і тому їх називають масовими подіями.
Подію називають масовою подією, якщо комплекс умов, що її породжує, можна повторити як завгодно багато разів (хоча б у принципі, теоретично).
Наприклад, масовими є наступні події: випадання герба при підкиданні монети; випадання “шістки” (шести очок) при киданні грального кубика; попадання в “десятку” під час пострілу по мішені тощо.
Зрозуміло, що масовою випадковою подією буде також випадання цифри (решки) при підкиданні монети. Нагадаємо, що решка – це лицьова сторона монети (аверс), на якій вибито її номінал, наприклад 1 гривня. Орел, герб – це зворотна сторона (реверс) монети.
Другою особливістю випадкових подій, що вивчаються в теорії ймовірностей, є статистична стійкість частот. Це означає, що при проведенні великої кількості випробувань відносна частота випадкової події (відношення числа появ події до загального числа випробувань) виявляє властивість стійкості, тобто стабілізується біля деякого числа, яке визначає ймовірність події.
Стійкість частот – це об’єктивна властивість масових випадкових явищ реального світу. Така властивість стійкості частот дозволяє досить точно прогнозувати властивості явищ, пов’язаних із даними випробуваннями.
Замість терміну “статистична стійкість” вживають також термін “статистична однорідність”.
Таким чином, предметом теорії ймовірностей є вивчення кількісних закономірностей, які характерні для масових однорідних випадкових подій.
Зазначимо, що теорія ймовірностей має справу не безпосередньо з явищами дійсності, реального світу, а з їх математичними моделями. У математичній моделі мають бути правильно передані суттєві сторони явища, що вивчається. Несуттєві сторони не враховують, відкидають. Занадто детальний опис явища призводить до ускладнення математичної моделі та може призвести до практичної неможливості її дослідження. Занадто спрощена модель може привести до хибних висновків. Тому вельми важливим є вибір “золотої середини”, тобто вибір адекватної моделі, яка, з одного боку, підлягає ефективному дослідженню математичними засобами, а з іншого – з високим ступенем точності описує реальні явища.
Наведемо схему, яка вказує на місце математичних моделей при дослідженні реальних явищ.
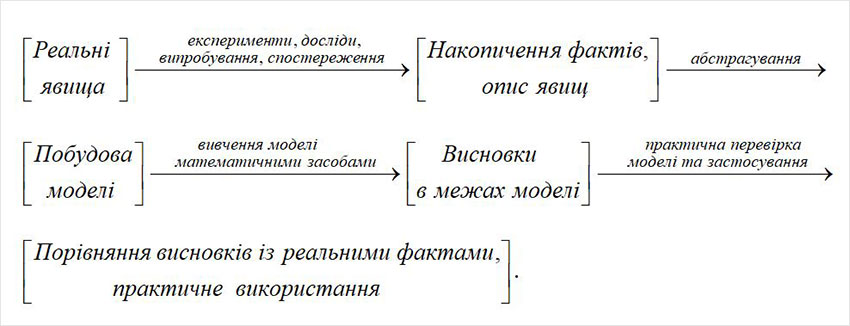
Таким чином, теорія ймовірностей – це математична наука, яка вивчає математичні моделі випадкових експериментів, тобто експериментів, наслідки яких не можна визначити однозначно умовами проведення експерименту. При цьому припускається, що сам експеримент можна повторити як завгодно багато разів (хоча б у принципі) при незмінному комплексі умов, а наслідки експерименту (випадкові події) мають статистичну стійкість.
Якщо говорити більш детально, то теорія ймовірностей встановлює такі зв’язки між ймовірностями випадкових подій у математичних моделях, які дозволяють обчислювати ймовірності складних подій за ймовірностями простих подій.
У теорії ймовірностей використовують результати і методи багатьох галузей математики (комбінаторики, математичного аналізу, алгебри, логіки та ін). Однак теорія ймовірностей має певну своєрідність, оскільки вона тісно пов’язана з різними застосуваннями, причому ці застосування не настільки звичні, як, наприклад, застосування диференціальних рівнянь.
Тому ефективно оволодіти теорією ймовірностей може лише той, хто розв’язує багато задач. Ці задачі часто мають “нематематичну” постановку і треба вміти будувати відповідну математичну модель. У результаті наполегливих дій із розв’язування задач і вивчення теоретичного матеріалу здобувається теоретико-ймовірнісна інтуїція та приходить досвід у використанні цієї науки на практиці.
Методи теорії ймовірностей широко застосовуються в різних галузях природознавства, техніки, економіки, гуманітарних науках. Багато вчених вважають, що в наш час відбувається “стохастична революція” у свідомості людського суспільства. Це обумовлено передусім тим, що багато подій і процесів у нашому житті мають випадковий характер.
Зазначимо, що теорія ймовірностей слугує також для обґрунтування математичної і прикладної статистики. Статистичні методи, у свою чергу, використовуються при плануванні та організації виробництва, для аналізу технологічних процесів, для контролю якості продукції та в інших цілях.
Предметом математичної статистики є дослідження статистичних закономірностей, яким підпорядковані масові випадкові явища. Ці дослідження проводять на підставі статистичних даних – результатів спостережень, а закономірності вивчають за допомогою методів теорії ймовірностей.
Таким чином, математична статистика виступає як цільове застосування теорії ймовірностей для дослідження статистичних даних з метою одержання наукових і практичних висновків щодо закономірностей масових випадкових явищ.
Зазначимо, що методи теорії ймовірностей і математичної статистики застосовуються в таких дисциплінах, як “Теорія надійності”, “Економетрія”, “Теорія ризику”, “Теорія масового обслуговування” та ін.
Широкому впровадженню математико-статистичних методів дослідження сприяла поява в другій половині ХХ ст. електронних обчислювальних машин і, зокрема, персональних комп’ютерів. Імовірнісно-статистичні програмні пакети зробили ці методи більш доступними і наочними, оскільки трудомістку роботу з розрахунку різних статистик, параметрів, характеристик, побудову таблиць і графіків став виконувати комп’ютер. А досліднику і користувачу комп’ютера залишилася головним чином творча робота: постановка задачі, побудова математичної моделі, вибір методів розв’язування та інтерпретація результатів.
“Наука про випадкове” досягла значних успіхів за кілька століть свого розвитку та ще не всі її вершини підкорено.
Література:
- Колмогоров А.Н. Основные понятия теории вероятностей. – М., 1974.
- Майстров Л.Е. Развитие понятия вероятности. – М., 1980.
- Гнеденко Б.В. Из истории науки о случайном. – М., 1981.
- Шмигевський М.В., Зелепугіна І.М., Попова Л.С. Теорія ймовірностей і математична статистика. – К., 2010.
М.В. Шмигевський, кандидат фізико-математичних наук




















 Засновник та видавець
Засновник та видавець