У початковій школі, де навчався хлопчик Карл Гаусc, майбутній знаменитий «король математики», вчитель, щоб зайняти клас на тривалий час, дав школярам самостійне завдання. Та маленький Гаус не залишив учителю жодних надій, виконавши завдання практично відразу.

Наведемо цю задачу, оскільки вона має деяке відношення до нашої розповіді. Потрібно обчислити суму всіх натуральних чисел від 1 до 100. Знаючі відразу зрозуміють, що задача – окремий випадок суми арифметичної прогресії з різницею 1, кожний наступний доданок ряду відрізняється від попереднього на 1.

Як, можливо, міркував Гаус. Він перегрупував суму, точніше, розбив її на пари чисел (у дужках, їх загалом – 49):

1 + 2 + 3 + ... + 100 = (1 + 99) + (2 + 98) +…
+ (49 + 51) + 50 + 100 = 5050.

У загальному випадку кожен наступний член прогресії дорівнює попередньому плюс різниця. Тобто n-й член прогресії u_n = u_n-1 + d, де d – різниця прогресії (у прикладі Гауса u₀ = 1, d = 1). Неважко знайти суму

s_n = (u₀ + u_n) + (u₁ + u_n-1) + …+ (u_n/2 + u_{n/2 +1}) =  (u₀ + u_n)×n/2.

Відповідь годиться як парних, так і непарних n.

А тепер, озброївшись здогадом К. Гауса, на простому фізичному прикладі вивчимо поняття визначеного інтегралу.

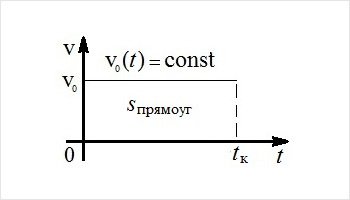
Почнемо з графіка руху з постійною швидкістю, див. рис.1, тобто рівномірного руху. Неважко знайти шлях, пройдений з такою швидкістю – це площа прямокутника зі сторонами v₀ і t_к:

s = v₀ t_к.

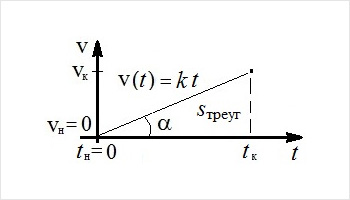
Постійну швидкість можна визначити як таку, за якої пройдений шлях пропорційний часу його проходження. Ускладнимо задачу, нехай швидкість лінійно змінюється з часом, рис.2. Звичайно, і в цьому випадку шлях знайти неважко. Для знаходження шляху нам знадобиться поняття середньої швидкості нерівномірного руху.

Середня швидкість нерівномірного руху – це швидкість такого рівномірного руху, коли за той самий проміжок часу, як і при нерівномірному русі, тіло проходить той самий шлях. У нашому випадку це площа трикутника, обмеженого залежністю v(t) = kt і віссю часу t. При цьому середня швидкість

 v_ср = (v_н + v_к)/2 = (0 + v_к)/2 = v_к/2,

де v_н і v_к – швидкість на початку та в кінці руху. Поняття середньої швидкості цікаве тим, що дозволяє замінити площу в загальному випадку криволінійного трикутника площею простого прямокутника висотою v_ср, Тоді шлях, пройдений за час Δt = t_к - t_н = t_к – 0 = t_к:

s = v_ср Δt = (v_к/2) t_к = (kt_к/2) t_к = kt_к²/2,

де t_н і t_к – початковий та кінцевий моменти часу руху.

З'ясуємо значення коефіцієнта k. Він дорівнює відношенню Δv/Δt = (v_к - v_н)/(t_к - t_н). У трикутнику на рис.2 (якщо зробити швидкість і час безрозмірними), – це відношення протилежного куту катета до прилеглого, тобто, тангенс кута α. Чим більший кут, тим швидше змінюється швидкість.

Далі вчинимо, можливо, несподівано. Знайдемо пройдений шлях інакше, способом, який стане у нагоді і в складніших випадках. Таким способом користувався великий давньогрецький учений Архімед, коли шукав об'єм бочки.

А вчинив він так. Розбив бочку на шари. Об'єм кожного шару приблизно дорівнював об'єму циліндра. Як відомо, об'єм циліндра – це добуток площі його основи (кола) на висоту (товщину шару). Знайти об'єм шару неважко, знаючи (вимірявши) радіуси окремих шарів.

Чим більше шарів розбиття, тим точніше значення об'єму бочки отримаємо. При можливості необмежено збільшувати кількість шарів, можна отримати скільки завгодно точне значення об'єму. Тут уточнимо, реальна точність визначення об'єму залежить від точності вимірювань радіуса шару та його товщини.

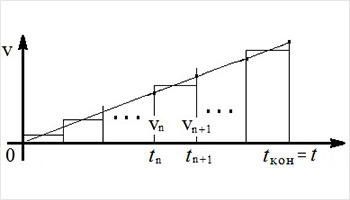
Діятимемо аналогічним чином. Виберемо ділянку шляху, на якому швидкість змінювалася від початкового значення v_н у момент t_н до кінцевого v_к у момент t_к, рис.3.

Розіб'ємо область під залежністю v(t) на N маленьких трапецій, заввишки Δt (на рис.3 – шириною). Так ми робимо тому, щоб став зрозумілим перехід до більш складної залежності v(t). Площа однієї трапеції – це шлях, який тіло пройде за час Δt. У довільної залежності верхня бічна сторона трапеції криволінійна. Інтервал часу руху теж розіб'ємо на однакові ділянки тривалістю Δt = (t_к – t_н)/N. Якщо t_к є деяке довільне t, а початкове значення дорівнює 0, то Δt = t/N.

Площа трапеції дорівнює площі прямокутника заввишки (v_n + v_n+1)/2 і шириною Δt. За умови, що число N дуже велике, v_n » v_n+1 і можна замінити (v_n + v_n+1)/2 на v_n.

Підрахувавши суму площ таких прямокутників, отримаємо повну площу під залежністю v(t). Але це і є повний шлях, пройдений тілом. Границю такої суми при N → ∞ якраз і називають інтегралом від функції v(t). У нашому випадку – це площа трикутника. Знайдемо цю площу – суму за всіма тимчасовими проміжками, починаючи з номера i = 0, потім 1, 2, ..., n, ... і до i = N, t_н = 0, t_к = t_N, t_n = nΔt и v(t_n) ≈ knΔt, маємо:

s ≈ ∑ v_nΔt  = ∑ knΔt Δt =

= k(Δt)²∑n = k(t/N)² (1 + 2 + 3+ ... + N) =

= k(t/N)² N(N+1)/2 = kt² N(N+1)/2N² = = (kt²/2)(1 + 1/N).

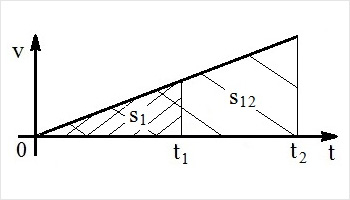
При N → ∞ s → kt²/2. Неважко знайти частину шляху між деякими моментами t₁ і t₂, дійсно s₁₂ = kt₂²/2 – kt₁²/2, геометрично, див. рис.4, – це площа трапеції s₁₂.

Для границі суми, що становить площу під залежністю v(t), І. Бернуллі, учень Г. Лейбніца, запропонував позначення «∫» (стилізована літера S – сума), так позначають інтеграл. За допомогою поняття інтеграл можна записати середню швидкість

v_ср = s/Δt = (1/Δt) ∫v(t)dt.

Якщо потрібно знати не середню швидкість на всьому шляху, а швидкість у малій, шириною ∂t околиці деякого моменту t, то слід шукати відношення ∂s/∂t. Чим менший інтервал ∂t поблизу моменту t, тим точніше визначається швидкість у точці (у певний момент часу) t. Це так звана миттєва швидкість. Таку операцію називають похідною від функції s(t) по t.

Найчастіше саме з цього поняття починають вивчати вищу математику. Ми приділили більше уваги операції інтегрування. Тим не менш, знайдемо похідну від швидкості у нашому прикладі. Маємо:

Δs/Δt = [s(t + Δt) - s(t)]/Δt = [k(t + Δt)²/2 - kt²/2]/Δt = k[2tΔt + (Δt)²]/2Δt = k[t + Δt/2]

при Δt → 0 отримаємо миттєву швидкість

lim (Δs/Δt) = kt = v(t).

Виявляється, таку властивість має довільна залежність v(t) (додамо: що має фізичний зміст, тобто допускає вимір). Отже, ми з'ясували, що шлях є інтегралом від швидкості, також швидкість є похідною від шляху за часом. Ми показали, що виконання операцій взяття інтеграла, з наступним знаходженням похідної залишають функцію без зміни. Це взаємно зворотні операції.

Математики записують цей факт, як добуток (послідовне дію) операторів D×D^–1f(x) = If(x) = f(x), де D и D^–1  – взаємно зворотні оператори інтегрування та взяття похідної (ця операція називається диференціюванням), I – одиничний оператор, що залишає функцію без змін.

Цікавий сенс цих операцій з точки зору точності вимірювань. Справа в тому, що з будь-яким ступенем точності фізична функція може бути представлена поліномом. Інтегрувати та диференціювати такі функції дуже просто, про що знали ще творці математичного аналізу Ісаак Ньютон та Готфрід Лейбніц, які дали загальний підхід до будь-яких задач із довільними функціями.

Для прикладу і на підтвердження наведених вище фактів, наведемо похідну від tⁿ по t (докладніше можна подивитися в будь-якому підручнику з математичного аналізу). Це такі формули:

 d(tⁿ)/dt = nt^n-1 і ∫tⁿdt = tⁿ⁺¹/(n + 1).

Очевидно, d(∫tⁿdt)/dt = tⁿ. Ця властивість доведена вище на прикладі n = 1. Якщо докласти невеликих зусиль, неважко перевірити наведені формули.

Перейдемо до другої частини назви нашого оповідання. Інтеграл, як і похідна, – це граничні операції, що передбачають можливість безмежного поділу інтервалу зміни незалежних змінних. У нашому прикладі ці змінні – швидкість та час.

Застосування у фізиці та техніці зазначених граничних операцій призвело, після тривалого застою, до революційних перетворень у житті людини. Успіхи були настільки вражаючими, що багато сучасних учених перейнялися переконанням, що зовсім небагато зусиль – і буде створена універсальна теорія всього, що пояснює будь-які фізичні явища.

В основі такої впевненості лежить, звичайно, суттєво вдосконалений аналіз нескінченно малих, про найважливіші поняття якого розказано вище.

Спроби створення такої теорії одним із перших зробив класик фізичної науки Альберт Ейнштейн. Спочатку його зусилля приймали за дивацтва генія, який займався створенням єдиної теорії поля практично в гордій самоті. Але до теперішнього часу все більше вчених робить спроби в цьому напрямку.

Подібні зусилля нам видаються наївними. Спробуємо захистити цю думку. І тут нам допоможе теорія непрямих вимірів. Що таке гранична операція інтегрування чи диференціювання (взяття похідної)? Далі ми розглянемо ці операції з погляду їх застосування до фізики.

Основа фізики – вимір. Зазначені операції при їх використанні в додатках є прикладом непрямих вимірювань. Нагадаємо, що непрямий вимір, це насправді обчислення значення фізичної величини за формулою. Причому у формулу входять величини, які можна безпосередньо виміряти з досвіду.

Для оцінки точності значення, розрахованого за формулою, ми колись запропонували принцип непрямої спостережуваності. Нагадаємо, у чому його суть. Відносна похибка непрямого виміру не повинна перевищувати жодну з відносних похибок величин прямих вимірів, які входять до опосередкованого виміру (у відповідну формулу).

Цей принцип підтверджує очевидну думку: ніякий вимір не можна виконати з якою завгодно високою точністю. Це твердження впритул підводить нас до підтвердження нездійсненності надій створення теорії всього.

Справа в тому, що будь-яка сучасна теорія мікросвіту, що претендує на завершеність, сьогодні використовує аналіз нескінченно малих з його граничними операціями, про які власне і йшлося вище.

І якщо для опису звичайних випадків, коли абсолютні похибки виміру значно менші вимірюваних величин, граничні операції призводять до гарної згоди з досвідом, то при описі явищ мікросвіту, коли точність приладів на межі можливостей вимірювання, використання зазначених операцій стає абсолютно необґрунтованим.

Міркування сучасної квантової теорії, засновані на використанні «класичних приладів» (інших просто немає), які нібито збурюють квантовий об'єкт, просто наївні. Як можна говорити про збурення того, що в принципі не може спостерігатися.

Напрошується єдиний висновок: будь-які теорії всього, які використовують граничні операції, що передбачають як завгодно високу, тобто недосяжну, точність вимірювання (обчислення), не можуть бути правильними. Це в кращому випадку красиві творіння людської логіки, засновані на теорії нескінченних множин Г. Кантора.

Можна привести ще один аргумент в обґрунтування наших міркувань. Висновок зі знаменитої теореми Банаха-Тарського, кажучи простою мовою, є те, що з одного апельсина, перегрупувавши окремі його частини (множину його точок), можна зібрати два і більше точно таких же апельсинів.

У даному разі логічно бездоганна конструкція (доказ теореми), зі застосуванням   взаємно-однозначної відповідності теорії Р. Кантора нескінченних множин, очевидно, призводить до протиріччя зі здоровим глуздом. І причина та сама – у використанні граничних операцій.

Як бачите, тут є над чим поміркувати юному (і не лише) читачеві. І автору залишається тільки побажати успіхів тому, хто зацікавиться темою нашої розповіді і замислиться над невичерпними загадками природи, яких завжди буде достатньо для всіх майбутніх поколінь учених.

О.М. Пальті, ст. наук. співр. з фізики ВТСП