Стародавні греки приписували легендарному Прометею, серед інших його безсмертних діянь, винайдення числа. Піфагор (VI ст. до н.е.) та його учні надавали числам дуже великого значення, вважаючи, що за їхньою допомогою можна виразити всі закономірності Всесвіту.

Особливу увагу піфагорійці приділяли натуральним числам і дробам. Серед найбільш значимих для них чисел були так звані «досконалі числа», які дорівнюють сумі всіх своїх дільників (менших самого числа). Наприклад, 6 – досконале число, тому що 6 = 1+2+3. Число 28 – також досконале, тому що виконується рівність 28 = 1+2+4+7+14.

Досконалий характер чисел 6 і 28, що мав велике математичне значення для піфагорійців, був також визнаний іншими культурами, які звернули увагу на те, що Місяць обертається навколо Землі кожні 28 днів, і які стверджували, що Бог створив світ за 6 днів.

У творі «Град Божий» Св. Августин висловив думку про те, що хоча Бог міг створити світ в одну мить, Він вирішив створити його за 6 днів, щоб за цей час подумати над досконалістю світу. На думку Св. Августина, число 6 досконале не тому, що Бог вибрав його, а тому, що досконалість внутрішньо притаманна природі цього числа.

По мірі того, як натуральні числа зростають, досконалі числа зустрічаються все рідше. Рено Декарт навіть стверджував, що «досконалі числа, подібно досконалим людям, зустрічаються дуже рідко». Третє досконале число 496, четверте – 8128, п’яте – 33 550 336, шосте – 8 589 869 056. Було помічено, що досконалі числа не лише дорівнюють сумі своїх дільників, але й мають інші цікаві властивості. Наприклад, досконалі числа завжди дорівнюють сумі декількох перших послідовних натуральних чисел. Дійсно, легко перевірити, що

6 = 1+2+3;
28 = 1+2+3+4+5+6+7;
496 = 1+2+3+4+5+6+7+...+30+31;
8128 = 1+2+3+4+5+6+7+..+126+127.

Піфагор не лише бавився з цими числами та колекціонував їх, він прагнув відкрити більш глибоке значення таких чисел. Одне з його відкриттів полягало в тому, що досконалість чисел тісно пов’язана з «двійковістю». Піфагор помітив, що всі степені числа 2 трішки не «дотягують» до того, щоб стати досконалими, оскільки сума їхніх дільників завжди на одиницю менша самого числа. Дійсно,

2² = 2∙2 = 4, дільники: 1,2, сума дільників  3,
2³ = 2∙2∙2 = 8, дільники: 1,2,4, сума дільників  7,
2⁴ = 2∙2∙2∙2 = 16, дільники: 1,2,4,8, сума дільників 15,
2⁵ = 2∙2∙2∙2∙2 = 32, дільники: 1,2,4,8,16, сума дільників  31.

Двома століттями пізніше Евклід (IV ст. до н.е.) уточнив помічений Піфагором взаємозв’язок між двійковістю і досконалістю. Евклід відкрив, що досконалі числа завжди кратні двом числам, одне з яких дорівнює степеню числа 2, а інше – на одиницю менше наступного степеня числа 2:

6 = 2¹ ∙ (2² – 1),  28 = 2² ∙ (2³ – 1),  496 = 2⁴ ∙ (2⁵ – 1),  8128 = 2⁶ ∙ (2⁷ – 1).

Отже, Евклід отримав такий результат: число вигляду

n = 2p-1 (2p - 1)

(1)

є досконалим, при умові, що число (2^p - 1) є простим.

Ця формула (1) увійшла в історію науки під назвою формули Евкліда.

Очевидно, що формула Евкліда визначає лише парні досконалі числа. І до того ж, Евклід довів твердження лише в одну сторону: якщо число n має вигляд (1) і при цьому (2^p - 1) є простим, то число n – досконале.

Питання про те, чи є справедливим обернене твердження, залишалось відкритим протягом двох тисячоліть. І лише Леонард Ейлер (1707–1783) встановив, що будь-яке досконале парне число має вигляд (1), при умові, що число (2^p - 1) є простим. Однак навіть Ейлер не зміг вказати жодного непарного досконалого числа або довести, що непарних досконалих чисел взагалі не існує.

У формулі Евкліда (1) суттєвою є вимога, що число (2^p - 1) є простим. Числами такого вигляду багато часу займався французький математик Марен Мерсенн (1588–1648), відомий також своїми перекладами праць давньогрецьких математиків. Мерсенн створив науковий гурток, який згодом став основою створення Паризької Академії наук. На його честь числа вигляду (2^p - 1) було названо «числами Мерсенна».

І тому результат Ейлера можна переформулювати таким чином: будь-яке парне досконале число задається формулою Евкліда (1), при умові, що відповідне число Мерсенна є простим.

Однак запитання: «скільки існує простих чисел Мерсенна?» до цього часу ще є відкритим. Отже, відкритим залишається й запитання: скільки існує парних досконалих чисел?

Зазначимо, що на сьогоднішній день знайдено трохи більше тридцяти парних досконалих чисел. Перші чотири досконалі числа знав ще Евклід (вони наведені в його «Началах»). П’яте досконале число 2¹²(2¹³ - 1) = 33 550 336 знайшов німецький математик Регіомонтан (XV ст.), який, між іншим, одним з перших у своїх працях застосовував знаки + і –.

У XVI ст. німецький учений Іоганн Ефраім Шейбель знайшов ще два досконалі числа (шосте і сьоме): 8 589 869 056 і 137 438 691 328. Ці числа отримуються за формулою (1) відповідно при p = 17 і p = 19. Восьме досконале число знайшов Ейлер при p = 31, а саме: 2 305 843 008 139 952 128.

Дев’яте досконале число знайшов російський математик-самоук Іван Михайлович Первушин у 1883 р. Він строго довів, що число Мерсенна (2⁶¹ - 1) є простим, а звідси вже легко випливало, що число 2⁶⁰(2⁶¹ - 1) є досконалим (це число містить 37 цифр).

Наступні досконалі числа були знайдені вже у ХХ ст. Звичайно, більш швидкому просуванню у знаходженні цих чисел сприяв розвиток комп’ютерної техніки. Однак і за допомогою надпотужних комп’ютерів вдалося знайти лише трохи більше тридцяти досконалих чисел. Наприклад, 32-е досконале число, знайдене в 1992 р., містить 455 663 цифри (воно отримується з формули (1) при p = 756 839).

Звичайно, ніякий комп’ютер не може знайти нескінченну кількість досконалих чисел – для цього необхідна вся міць і геніальність людського розуму, щоб теоретичним шляхом розв’язати проблеми, які протягом багатьох століть кидають виклик людству.

Проблема 1. Скінченна чи нескінченна множина парних досконалих чисел?

Проблема 2. Скінченна чи нескінченна множина простих чисел Мерсенна?

Проблема 3. Знайти хоча б одне непарне досконале число.

До речі, Декарт запевняв, що розв’яже проблему 3 за три місяці «творчої відпустки». Однак з тих часів минуло вже майже п’ять століть, а проблема все ще залишається недосяжною...

Перейдемо тепер до узагальнення поняття досконалого числа. Ще піфагорійці ввели до розгляду так звані «дружні числа» – це такі пари натуральних чисел, кожне з яких дорівнює сумі всіх дільників іншого (менших самого числа). Піфагорійці знали лише одну пару дружніх чисел – 220 та 284 – і вважали їх символом дружби.

220 = 1+2+4+71+142;
284 = 1+2+4+5+10+11+20+22+44+55+110.

Піфагор стверджував: «Мій друг той, хто є моїм другим «я», як числа 220 і 284». Довго вважалось, що наступну пару дружніх чисел 17296 і 18416 відкрив у 1636 р. знаменитий французький математик П'єр Ферма. Але нещодавно в одному з трактатів арабського вченого Ібн аль-Банни (1256–1321) було знайдено рядки: «Числа 17296 і 18416 є дружними. Аллах всеосяжний».

А задовго до Ібн аль-Банни інший арабський математик, астроном, механік, медик і філософ Абу-л-Хасан Сабіт Ібн Курра (836–901) сформулював правило, за яким можна отримати деякі дружні числа:

якщо для деякого натурального n числа p, q, r – прості, то числа A, B – дружні,

де p = 3 × 2 ^{n - 1} - 1, q = 3 × 2 ⁿ - 1, r = 9 × 2 ^{2n – 1} - 1, A = 2 ⁿ × pq, B = 2 ⁿ  × r.

До речі, саме Сабіт Ібн Курра переклав «Начала» Евкліда арабською мовою, написав коментарі до них і ознайомив арабських учених із трактатом Архімеда про правильні семикутники (грецький текст трактату до цього часу не знайдено).

Користуючись формулою Сабіта, можна отримати деякі дружні числа.

При n = 2 числа p = 5, q = 11, r = 71 є простими, і тому отримаємо пару дружніх чисел А = 220 і В = 284 (числа, знайдені Піфагором).

При n = 4 числа p = 23, q = 47, r = 1151 є простими, і тому отримаємо пару дружніх чисел А = 17296 і В = 18416 (числа, знайдені Сабітом, а згодом і П. Ферма).

При n = 7 отримаємо пару дружніх чисел, знайдених у 1638 р. французьким математиком і філософом Рене Декартом: А = 9363584, В = 9437056.

На початку XVII ст. П. Ферма (1636 р.) і Р. Декарт (1638 р.), незалежно один від одного, а також від Сабіта, перевідкрили формули Сабіта (доведено, що їм був невідомим факт існування цих формул, знайдених ще в IX ст.).

Після Декарта першим отримав нові дружні числа Л. Ейлер. Він відкрив 59 пар дружніх чисел, серед яких були і непарні числа, наприклад, 9773505 і 11791935. Він також запропонував п’ять способів відшукання дружніх чисел. Ці дослідження продовжили математики наступних поколінь.

У наш час відомо біля 1100 пар дружніх чисел. У 1867 р. 16-річний італієць Б. Паганіні здивував математичний світ повідомленням про те, що числа 1184 і 1210 – теж дружні! Цю пару, найближчу до 220 і 284, прогледіли всі знамениті попередники. У добу Середньовіччя дуже популярними були талісмани з вигравійованими на них числами 220 і 284, які нібито сприяли зміцненню дружби і кохання.

Дружні числа продовжують приховувати багато таємниць. Наприклад, невідомо, чи існують пари, в яких одне число парне, а інше – непарне? Скінченна чи нескінченна множина пар дружніх чисел? Чи існує загальна формула, яка дозволяє описати всі пари дружніх чисел?

Цікаву пару дружніх чисел знайшов у 1972 р. амстердамський математик Херман те Риле. Кожне з цих чисел містить по 152 цифри у десятковому запису. У першого числа 800 різних дільників, у другого – 3200. А взагалі світовий рекорд належить американському математикові Елвіну Дж. Лі – він за допомогою комп’ютера знайшов 390 пар дружніх чисел.

У XX ст. математики узагальнили поняття дружніх чисел і зайнялись пошуком дружніх рядів (інша назва – товариські числа або числа, що спілкуються між собою) – це замкнені цикли з трьох та більше чисел. Наприклад, у трійці чисел

1945330728960;  2324196638720;  2615631953920

дільники першого числа в сумі дають друге число, дільники другого в сумі дають третє число, а дільники третього числа в сумі дають перше число.

Наведемо ряд із п’яти дружніх чисел: 12496, 14288, 15472, 14536, 14264.

Найдовший із відомих циклів складають 28 чисел, перше з яких дорівнює 14316. Відкритим залишається питання про те, скінченна чи нескінченна множина дружніх рядів чисел, а також, чи існують дружні ряди довільної наперед заданої довжини (наприклад, існує гіпотеза, що цикл з 100 чисел не може утворювати дружній ряд).

Проблема 4. Скінченна чи нескінченна множина пар дружніх чисел?

Проблема 5. Знайти загальну формулу для отримання всіх пар дружніх чисел.

Деякі не розв’язані проблеми пов’язані з множиною простих чисел: 2, 3, 5, 7, 11, 13, ... (кожне просте число має лише два натуральних дільники – одиницю і саме число). Евклід у IV ст. до н.е. довів, що простих чисел є нескінченно багато. Його доведення стало зразком математичної вишуканості.

Математики протягом століть прагнули розгадати закон, за яким розподілені прості числа. Деякі вчені шукали формули, які б давали прості числа. Наприклад, Ейлер склав формулу p = n² – n + 41, яка при n = 0, 1, 2, 3,..., 39, 40 дає прості числа. Але вже при n = 41 ця формула дає складене число p = 41∙41.

Було також вказано дещо складнішу формулу p = n² – 79n + 1601, яка дає прості числа при n = 0, 1, 2, 3,..., 78, 79. П. Ферма вважав, що знайшов формулу простого числа у вигляді F(n) = 2^k + 1, де k = 2ⁿ. Дійсно, при n = 0,1,2,3,4 вираз F(n) приймає значення 3,5,17,257,65537, які є простими числами. Однак, як показав Л. Ейлер, F(5) = 2³² + 1 – складене число. Числа вигляду  F(n) = 2^k + 1, де k = 2ⁿ, n = 0,1,2,3,..., називають числами Ферма.

Проблема 6. Скінченна чи нескінченна множина простих чисел Ферма?

Той факт, що не існує многочлена P(n) з цілими коефіцієнтами, всі значення якого при цілих n були б простими числами, довели Християн Гольдбах і Леонардо Ейлер. Пошуки загальної формули, яка при всіх n давала б просте число, виявились безрезультатними.

З XVIII ст. вчені почали шукати формулу, яка хоча б наближено виражала кількість простих чисел на даному проміжку. Позначимо через π(х) – кількість простих чисел, що не перевищують даного числа х > 0. Наприклад, π(1) = 0, π(2) = 1, π(3) = 2, π(4) = 2, π(5) = 3, …, π(100) = 25, … Точну формулу знайти не вдалося, тому всі зусилля були зосереджені на пошуку емпіричних формул, які дають наближення для π(х).

Карл Гаусс у 15-річному віці, аналізуючи таблиці простих чисел, що містилися в подарованій йому роком раніше таблиці логарифмів, емпірично прийшов до наближеної формули: π(х) » х/lnx. Французький математик Адрієн  Лежандр у 1798–1808 рр. знайшов, як йому здавалося, кращу емпіричну формулу: π(х) » х/(lnx – 1,08366). Згодом К. Гаусс вказав, що для знаходження кількості простих чисел на проміжку від одиниці до даного числа можна наближено користуватися логарифмічною сумою: p(х) » Ls(х), де Ls(x) = 1/ln2 + 1/ln3 + 1/ln4 + … + 1/lnx.

Як з’ясувалося дещо пізніше, наближення Лежандра лише при невеликих х (приблизно до 1 мільйона) є значно точнішим від наближення Гаусса, однак починаючи з 5 мільйонів ситуація змінюється навпаки: точність формули Гаусса зростає, у той же час точність формули Лежандра значно погіршується.

Видатний російський математик Пафнутій Львович Чебишев (1821–1894) показав у 1850 р., що емпірична формула Лежандра не є асимптотичною рівністю, глибоко дослідив властивості функції π(х) і встановив, що справжній порядок зростання цієї функції такий же, як і функції х/lnx. До того, ним було наведено оцінки: 0, 92129 < (π(х):х/lnx) < 1,10555.

Він також знайшов деякі інтегральні оцінки для p(х), з яких випливає асимптотична формула π(х) ~ Li(x), де Li(x) =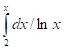 – інтегральний логарифм. При цьому мають місце такі нерівності: Ls(x) – 1,5 < Li(x) < Ls(x), тобто різниця Li(x) – Ls(x) є обмеженою. Зазначимо, що в наш час інтегральний логарифм визначають як функцію  li(x) =  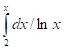(цей інтеграл розуміють у сенсі головного значення).

Строге доведення асимптотичної рівності π(х) ~ х/lnx запропонували в 1896 р. французький математик Жак Адамар і (незалежно) бельгійський математик Валле Пуссен (це було зроблене на основі досліджень Бернгарда Рімана з теорії функцій комплексної змінної). Тут знак ~ означає, що відношення виразів, які сполучено цим знаком, прямує до 1 при нескінченному зростанні х, тобто в нашому випадку (π(х):х/lnx) → 1 при х → ∞. Асимптотичну рівність π(х) ~ х/lnx називають у наш час законом розподілу простих чисел.

Пафнутій Львович Чебишев розв’язав також низку складних проблем теорії чисел, зокрема довів так званий «постулат Бертрана»: для всіх натуральних чисел n, починаючи з 4, між числами n і (2n – 2) міститься принаймні одне просте число.

Сам Бертран перевірив свою гіпотезу для всіх натуральних чисел до 6 000 000, але не зміг її довести для довільного n. П.Л. Чебишев за допомогою розроблених ним методів строго довів цю гіпотезу для довільного n і тим самим перетворив її в теорему.

Організація Electronic Frontier Foundation заснувала декілька призів для шукачів простих чисел за розв’язання наступної проблеми.

Проблема 7. Знайти прості числа, які містять у десятковому запису відповідно не менше 10, 100 і 1000 мільйонів цифр.

Розмір винагороди становить 100 000 доларів за знаходження простого числа, яке містить у десятковому запису не менше 10 мільйонів цифр, 150 000 доларів – не менше 100 мільйонів цифр і 250 000 доларів – не менше 1000 мільйонів цифр. Приз у 50 000 доларів 6 квітня 2000 року вже отримали ентузіасти, які відшукали просте число, що містить у десятковому запису 1 мільйон цифр. До речі, публікація такого простого числа зайняла б три номери нашого журналу.

Цікава проблема пов’язана з так званими «числами-близнюками». Два числа називають близнюками, якщо різниця між ними дорівнює 2, наприклад, (4; 6), (25; 27), ... – пари чисел-близнюків. Очевидно, що у множині натуральних чисел таких пар нескінченно багато. Однак задача стає занадто складною, якщо розглядати лише прості числа-близнюки, наприклад наступні пари: (5; 7), (11; 13), (17; 19),..., (101; 103), ...

Проблема 8 (проблема близнюків). Скінченна чи нескінченна множина пар простих чисел-близнюків?

На сьогодні відомі пари великих простих чисел-близнюків, наприклад: (22 271; 22 273),..., (1 000 000 000 061; 1 000 000 000 063). Останнім часом було знайдено таку пару: (260 497 545 ∙ 2⁶⁶²⁵ – 1;  260 497 545 ∙ 2⁶⁶²⁵ + 1). Деякі математики вважають, що простих чисел-близнюків нескінченно багато, але досі ніхто не може довести, що це справді так.

М.В. Шмигевський, кандидат фізико-математичних наук