Ідея, яка застосована лише раз, є штучною,
а застосована двічі – стає методом.
Упродовж століть у математиці створено потужний арсенал понять, методів та ідей, які дозволяють ефективно досліджувати проблеми як самої математики, так й інших природничих, технічних і соціальних наук.
Серед розмаїття математичних понять особливе місце посідає «велика трійця»: похідна, інтеграл та ряд. Перші два поняття в достатньому обсязі висвітлено в шкільному курсі математики. Третє з них, а саме поняття ряду, фактично застосовується лише при вивченні числових послідовностей, зокрема, нескінченно спадної геометричної прогресії.
Наше завдання полягає в тому, щоб показати взаємодію цих понять, ще раз підкреслити, що сила математики полягає в єдності та взаємодії її частин.
До речі, на одному з математичних конгресів провели опитування провідних математиків світу: яке поняття їхньої улюбленої науки є найбільш цінним як для математики, так і для її застосувань? Переважна більшість учених дала однозначну відповідь: числові та функціональні ряди.
Короткий історичний екскурс. Установити, коли вперше з’явилися ряди в математиці, мабуть, неможливо. Ще вавилонські математики вміли підсумовувати геометричну й арифметичну прогресії. Нескінченна геометрична прогресія була історично першим числовим рядом, для якого була знайдена його сума.
Архімед (ІІІ ст. до н.е.) для обчислення площі параболічного сегмента (тобто фігури, обмеженої прямою і параболою) застосував підсумовування нескінченної геометричної прогресії зі знаменником 1/4.
Після Архімеда і до ХVI ст. математики ряди не вивчали. Ряди увійшли в математику лише тоді, коли почалося активне вивчення змінних величин і процесів. Значний інтерес викликали задачі знаходження сум рядів. Приблизно 1500 р. індійські математики обчислили суму числового ряду
3
5
7
9
4
яку згодом незалежно знайшли Г. Лейбніц і Д. Грегорі.
Л. Ейлер знайшов суму ряду
12
22
32
42
52
6
хоча поняття збіжності ряду на той час точно встановлено ще не було. Вважалося, що будь-який ряд має суму і з рядами можна виконувати ті ж арифметичні дії, що й із многочленами: додавати, множити, переставляти доданки та ін.
Таке вільне тлумачення дій із рядами іноді призводило до курйозів і непорозумінь.
Наприклад, отримували, що сума ряду 1-1+1-1+1-1+… може дорівнювати як 0, так і 1, і навіть 0,5. Міркування були приблизно такими:
S=1-1+1-1+1-1+…=(1-1)+(1-1)+(1-1)+…=0,
S=1-1+1-1+1-1+1…=1-(1-1)+(1-1)+(1-1)+…=1,
S=1-1+1-1+1-1+…=1-(1-1+1-1+1+…)=1-S, тобто S=1-S, звідки 2S=1, S=0,5.
Наведені «міркування», звичайно, математично не коректні. Однак, це стало зрозумілим лише на початку ХІХ ст., коли було введено чітке поняття збіжності ряду, яке спиралося на поняття границі послідовності частинних сум ряду. Тоді ж і почалося систематичне вивчення рядів.
У наш час теорія рядів є однією з найбільш потужних галузей математики.
Тож спочатку введемо поняття ряду. У математиці числовим рядом називають вираз вигляду
a1+a2+a3+…+an+…,
складений із чисел a1, a2, a3, …, an, які називають членами ряду: a1 – перший член ряду, a2 – другий член ряду, …, an – n-й член ряду (цей член називають також загальним членом ряду).
Числовий ряд можна записувати в скороченому вигляді: ![]() .
.
Ряд вважається заданим, якщо задано правило, яке дозволяє за відомим номером його члена записати цей член ряду. Найчастіше ряд задається формулою загального члена an = f(n).
Важливим є те, що при утворенні ряду множина чисел a1, a2, a3, …, an, … обов’язково нескінченна. Таким чином, поняття ряду дозволяє узагальнити поняття суми на деякі випадки нескінченної множини доданків і вивчити властивості таких узагальнених сум.
Перше питання, яке виникає при вивченні рядів, полягає в тому, чи мають вони якесь числове значення. Виявляється, що приписати розумним чином таке значення можна далеко не всім, а лише так званим збіжним рядам.
Нехай задано ряд a1+a2+a3+…+an+…
Утворимо послідовність чисел S1, S2, S3, …, Sn, покладаючи S1 = a1, S1 = a1+a2, S2 = a1+a2+a3, … , Sn = a1+a2+a3+…+an .
Ці числа називають частинними сумами ряду.
Якщо існує скінченна границя ![]() , то ряд називають збіжним, а число S називають сумою ряду. У цьому разі пишуть:
, то ряд називають збіжним, а число S називають сумою ряду. У цьому разі пишуть: ![]() .
.
Таким чином, сума ряду – це скінченна границя послідовності його частинних сум.
Ряд називають розбіжним, якщо ![]() не існує (зокрема, якщо
не існує (зокрема, якщо ![]() ). Якщо ряд розбіжний, то йому не приписують ніякого числового значення.
). Якщо ряд розбіжний, то йому не приписують ніякого числового значення.
Для деяких рядів їхні суми можна знаходити оригінальними способами, враховуючи специфіку формули загального члена і минаючи складну процедуру обчислення частинних сум і відповідних границь. Проілюструємо вищесказане на кількох прикладах, застосовуючи різні ідеї.
Для демонстрації першої ідеї розв’яжемо відому задачу – обчислимо суму нескінченної спадної геометричної прогресії:
2
22
23
24
Помітивши, що половина шуканої суми
2
22
23
24
25
відрізняється від S на 1/2, отримаємо рівняння:
S – 0,5·S = 0,5, звідки: S = 1.
Аналогічна ідея спрацьовує і в наступному прикладі – при обчисленні суми ряду 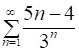 , загальний член якого
, загальний член якого 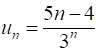 дорівнює відношенню відповідних членів арифметичної і геометричної прогресій. Маємо:
дорівнює відношенню відповідних членів арифметичної і геометричної прогресій. Маємо:
3
32
33
34
35
3
32
33
34
35
36
Віднявши від першої суми другу (і звівши при цьому доданки зі спільними знаменниками), отримаємо:
3
3
32
33
34
35
тобто
3
3
32
33
34
35
Вираз у квадратних дужках обчислимо як суму спадної геометричної прогресії з першим членом b1 = 1/9 і знаменником q = 1/3:
32
33
34
35
1 - 1/3
6
Отже, (2/3)·S =1/3 + 5·(1/6), звідки 4S = 2+5, і остаточно: S = 7/4.
Зауважимо, що так можна отримати і загальну формулу:
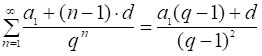 [*]
[*]
Якщо в цій формулі покласти a1=1, d=5, q=3, то отримаємо результат попереднього прикладу:
3
32
33
34
35
(3-1)2
4
Розглянемо ще один приклад. Обчислимо суму 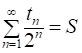 , де tn – трикутні числа. Запишемо шукану суму так:
, де tn – трикутні числа. Запишемо шукану суму так:
2
22
23
24
25
26
27
2n
тоді вдвічі менша сума дорівнюватиме:
2
22
23
24
25
26
27
2n
Розглянемо різницю сум [1] і [2]: S – 1/2·S = S/2. Звівши доданки зі спільними знаменниками, отримаємо:
 . [3]
. [3]
Зрозуміло, що сума, вдвічі менша, ніж сума [3], дорівнюватиме:
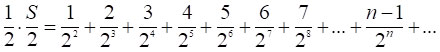 . [4]
. [4]
Розглянемо різницю сум [3] і [4]: S/2 – 1/2·S/2 = S/4. Звівши доданки зі спільними знаменниками, отримаємо:
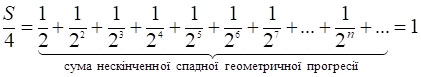
Отже, з останньої рівності маємо: S/4 = 1, звідки
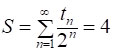 . [5]
. [5]
Враховуючи результат [5], із рівності [3] отримаємо:
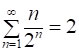 [6]
[6]
Результат можна було б отримати (як перевірка) й іншим способом – поклавши у формулі [*] a1=1, d=1, q=2, тоді:
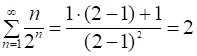 .
.
Додавши праві частини рівностей [1] і [2], (і звівши при цьому доданки зі спільними знаменниками) легко отримати:
![]() ,
,
тобто: 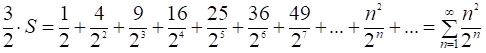 ,
,
звідки, враховуючи результат [5], отримаємо:
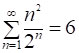 . [7]
. [7]
Контроль обчислень: з одного боку, враховуючи рівності [7] і [6], маємо:
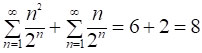 .
.
З іншого боку, враховуючи рівність [5], отримаємо той самий результат:
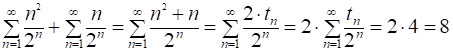 .
.
Зауважимо, що результат [6] можна отримати й іншим способом, що ґрунтується на не менш красивій ідеї, і до того ж – як наслідок більш загального результату.
Знайдемо суму ![]() для всіх x, які задовольняють умову │x│< 1.
для всіх x, які задовольняють умову │x│< 1.
Зрозуміло, що при x=1/2 отримаємо вихідну задачу і вже відомий результат [6]. Запишемо шукану суму в «розгорнутому» вигляді:
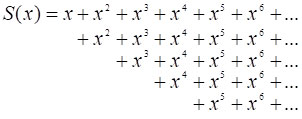
і обчислимо суму кожного рядка як суму нескінченної спадної геометричної прогресії, у якої знаменник q = x (│q│< 1). Як відомо, 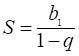 .
.
1 - x
1 - x
1 - x
1 - x
Додавши отримані суми «у стовпчик», отримаємо:
1-x
1-x
1-x
1-x
1 - x)
1-x
(1-x)2
Отже, S(x)=x/(1-x)2; і остаточно:
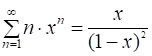 , │x│<1. [6*]
, │x│<1. [6*]
Контроль обчислень: поклавши у формулі [6*] x=1/2, отримаємо вже відомий нам результат [6]: 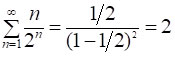 .
.
Зауважимо, що результат [6*] можна отримати й іншим способом (з використанням похідної), який коротко можна записати так:
![]()
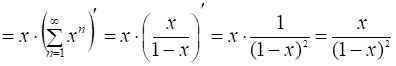 .
.
Узагальнимо тепер результат [7], знайшовши суму:
![]()
для всіх x, які задовольняють умову │x│<1.
Зрозуміло, що при x=1/2 отримаємо вихідну задачу і вже відомий результат [7].
Нехай ![]() ;
;
тоді вихідна задача полягатиме в знаходженні суми S(x). Маємо:
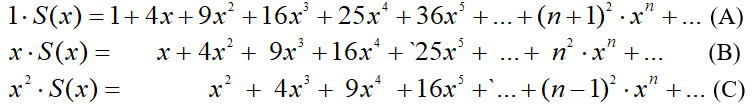
Розглянемо суму, утворену наступним чином: від сум (A) і (C) відняли подвоєну суму (B). Коефіцієнти в розглядуваній сумі при xn для всіх n≥1 дорівнюють числу два. Справді, xn:
(n+1)2+(n–1)2–2n2=2.
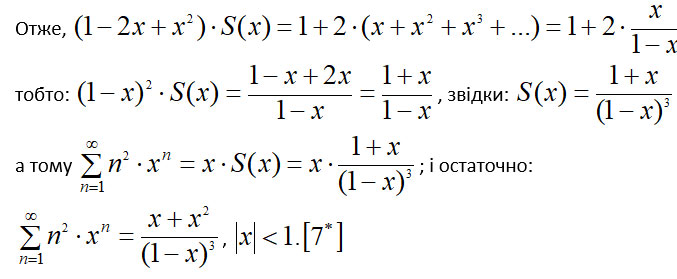
Контроль обчислень: поклавши у формулі [7*] x=1/2, отримаємо вже відомий нам результат [7]: 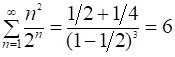 .
.
Зауважимо, що результат [7*] можна отримати й іншим способом (з використанням похідної і результату [6*]), який коротко можна записати так:
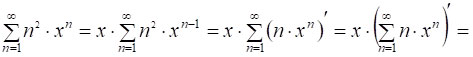
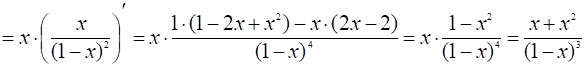 .
.
Розв’язання наступних двох задач ґрунтується на вже знайомій нам оригінальній ідеї.
1. Знайти суму:
![]() , │x│<1.
, │x│<1.
Розв’язання. Мають місце рівності:
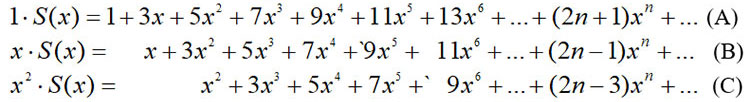
Розглянемо ряд, утворений наступним чином: від суми рядів (A) і (C) відняли подвоєний ряд (B). Коефіцієнти цього ряду при xn для всіх n≥2 дорівнюють нулю. Справді, xn: (2n+1)+(2n–3)–2(2n–1)=0.
Таким чином, (1–2x+x2)·S(x)=1+x. Відповідь: S(x)=(1+x)/(1–x)2.
2. Знайти суму:
S(x)=1+x+2x2+4x3+7x4+13x5+24x6+… (│x│<1), у якій коефіцієнт кожного наступного доданка дорівнює сумі трьох попередніх.
Розв’язання. Маємо:
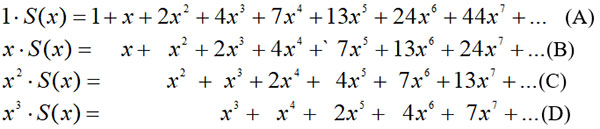
Віднявши від ряду (А) ряди (В), (С) і (D), отримаємо співвідношення: (1–x–x2–x3)·S(x)=1. Відповідь: S(x)=1/(1–x–x2–x3).
Обчислимо суму 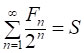 , де чисельники доданків утворюють послідовність Фібоначчі, тобто послідовність, в якій перший член F1=1, другий член F2=1, а кожний наступний член, починаючи з третього, дорівнює сумі двох попередніх: │Fn= Fn-1+ Fn-2│, n=3,4,5,…
, де чисельники доданків утворюють послідовність Фібоначчі, тобто послідовність, в якій перший член F1=1, другий член F2=1, а кожний наступний член, починаючи з третього, дорівнює сумі двох попередніх: │Fn= Fn-1+ Fn-2│, n=3,4,5,…
Розв’язання. Запишемо шукану суму так:
2
22
23
24
25
26
27
2n
2
22
23
24
25
26
27
2n
Розглянемо різницю лівих частин рівностей [8] і [9]: S – (1/2)·S = S/2; та різницю правих частин рівностей [8] і [9] (при цьому звівши доданки зі спільними знаменниками).
Отже,
2
2
4
2
22
23
24
25
26
2n-2
Таким чином, маємо рівняння відносно шуканої суми S: S/2 = 1/2 + S/4, звідки 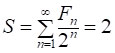 [10].
[10].
І наостанок, обчислимо суму 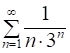 .
.
Розв’язання. Знайдемо більш загальну суму 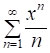 (де │x│<1 ), з якої при x=1/3 можна буде отримати і шуканий результат.
(де │x│<1 ), з якої при x=1/3 можна буде отримати і шуканий результат.
Очевидно, що 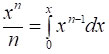 , тому:
, тому:
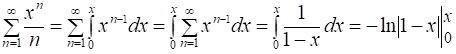 .
.
Таким чином, 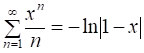 . Покладаючи в останній рівності x=1/3,
. Покладаючи в останній рівності x=1/3,
маємо: 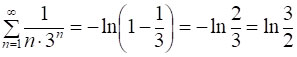 .
.
Відповідь: ln(3/2).
О.О. Мазурок, канд. фіз.-мат. наук, М.В. Шмигевський, канд. фіз.-мат. наук




















 Засновник та видавець
Засновник та видавець