Відшукай всьому початок, і ти багато чого зрозумієш.
К. ПрутковЯке вміння найважливіше?
– Вміння запитувати.
Що таке оптимізація взагалі? Найбільш просто – це вибір найкращого варіанта з безлічі можливих за деяким критерієм. Якщо критерій вибору відомий і варіантів небагато, то рішення може бути знайдене шляхом простого перебору і порівняння всіх варіантів. Однак часто буває так, що число можливих варіантів настільки велике, що повний перебір практично неможливий. У таких випадках доводиться формулювати завдання на мові математики і застосовувати спеціальні методи пошуку оптимального рішення, тобто методи оптимізації.
Однією з основних задач оптимізації є так звана задача математичного програмування, яка в загальному випадку полягає в знаходженні такого вектора х = (х1,х2,…,хn), при якому досягається найбільше або найменше значення неперервної функції f(x), за умови, що x ∈ M, де M – допустима область, яка є деякою підмножиною всього простору.
Математична форма запису цієї задачі (для визначеності сформулюємо її як задачу максимізації, хоча вона нічим не відрізняється від задачі мінімізації) така:
max{f(x) | x ∈ M}.
Функцію f(x) називають цільової, а умови, що описують множину М – системою обмежень. Залежно від виду цієї функції і властивостей допустимої області M задача математичного програмування відноситься до того чи іншого класу. Існують різні принципи класифікації задач математичного програмування. Однією з найважливіших задач математичного програмування є задача лінійного програмування – в ній цільова функція і система обмежень є лінійними функціями.
У теорії і практиці математичного програмування важливу роль відіграють задачі цілочислового (дискретного) програмування, коли всі змінні в задачі повинні набувати тільки цілочислових (не дробових) значень. Це пов'язане з фізичною неділимістю багатьох об'єктів розрахунку.
Всі методи дискретної оптимізації і відповідні їм алгоритми по основній ідеї кожного з них можна розділити на три великі групи:
• відсікання;
• комбінаторні (переборні);
• наближені.
Зупинимося докладніше на цих методах.
(1914-2005)
1. Методи відсікання. Історично дослідженням задач дискретної оптимізації передував розвиток теорії і методів лінійного програмування, зокрема, створення Джорджем Данцігом симплекс-методу як універсального методу рішення задач лінійного програмування. Природними були спроби подати вихідну дискретну задачу як задачу цілочислового лінійного програмування і звести її рішення до використання вже наявних методів рішення безперервних лінійних задач, зокрема, симплекс-методу. Однак просте округлення одержуваних значень змінних не призводило до успіху.
Тому була розроблена складніша процедура рішення цілочислової задачі лінійного програмування, відома під назвою методу відсікання.
Методи відсікання зводять рішення задачі цілочислового лінійного програмування до рішення послідовності спеціальним чином побудованих задач лінійного програмування. Вперше ця ідея для задач цілочислового лінійного програмування була висловлена тим же Дж. Данцігом.
Вона полягає в наступному. Якщо отримане рішення задовольняє умову цілочисловості, то процес закінчено. В іншому випадку до обмежень вихідної задачі додається нове лінійне обмеження, що має дві властивості:
• отримане нецілочислове рішення їй не задовольняє;
• будь-яке цілочислове рішення їй задовольняє.
Далі знову розв’язується задача лінійного програмування з додатково введеним обмеженням (відсіканням), процес повторюється до отримання цілочислового рішення.
Іншими словами, відсікається непотрібне рішення безперервної задачі і виключається можливість втрати рішення цілочислової задачі. Знову вирішується задача без умови цілочисловості. Процес триває доти, поки оптимальне рішення не виявиться цілочисловим.
Реалізація методу відсікання передбачає вирішення таких трьох проблем:
• знаходження універсального правила формування відсікань;
• доказ скінченності процесу відсікання;
• боротьба з надмірним зростанням розмірності задач при додаванні обмежень.
Ці проблеми вперше були вирішені за допомогою алгоритмів Р. Гомори, який сформулював універсальне правило формування відсікань і довів скінченність процесу відсікань.
Однак у подальшому виявилася велика непередбачуваність у поведінці різних алгоритмів відсікання. Виявилося, що кількість кроків істотно залежить не тільки від розмірності задачі, але і від конкретних числових даних. Були виявлені задачі відносно невеликої розмірності, рішення яких вимагає великих витрат машинного часу.
Надалі методи відсікання не знайшли широкого застосування при розв’язку прикладних задач цілочислового лінійного програмування з таких причин:
• складно визначити, яке відсікання (з великої їх кількості) є найкращим;
• методи відсікання пристосовані в основному для вирішення суто цілочислових задач, які складають лише малу частину задач, що зустрічаються в додатках;
• методи відсікання не пристосовані для розв’язку розріджених задач цілочислового лінійного програмування.
2. Комбінаторні (переборні) методи. Тут необхідно спочатку визначити поняття оптимізаційно-комбінаторної задачі. Це можна зробити таким чином.
Нехай є множина з n елементів. На цій множині задається безліч комбінацій P = {p1, p2, ..., pn}, де під комбінаціями розуміються поєднання, підстановки, перестановки, властиві кожній конкретній задачі. На множині Р задається деяка функція f. В оптимізаційно-комбінаторній задачі шукають екстремум функції f (максимум або мінімум) і відшукують ті елементи множини P, на яких функція f є екстремальною.
Наведемо, як приклад, популярну задачу про ранець (або рюкзак), яка отримала назву від кінцевої мети: укласти якомога більше цінних речей у рюкзак за умови, що місткість рюкзака обмежена. У різних варіаціях із задачею про рюкзак можна зіткнутися в економіці, прикладній математиці, криптографії та логістиці.
У загальному вигляді задачу можна сформулювати так: із заданої множини предметів з властивостями «вартість» і «вага» потрібно відібрати підмножину з максимальною повною вартістю, дотримуючись при цьому обмеження на сумарну вагу.
При вирішенні оптимізаційно-комбінаторних задач необхідно:
• вміти перебирати безліч значень функції f;
• обчислювати ці значення і порівнювати.
Для рішення оптимізаційно-комбінаторних задач було розроблено велику кількість методів, основна ідея яких полягає у використанні скінченної множини допустимих рішень і заміні повного їх перебору скороченим (спрямованим або неявним перебором). Головну роль у скороченні перебору грають оцінка і відкидання неперспективних підмножин, які заздалегідь не містять оптимальних рішень. Відкидання таких підмножин дозволяє замінити повний перебір частковим і тим самим зменшити витрати обчислювальних ресурсів.
Комбінаторні методи розрізняються способом розбиття і способом оцінювання, ці способи, зазвичай, пов'язані зі специфікою розв'язуваних класів задач. Правила, відповідно до яких проводиться відсів підмножин, які заздалегідь не містять оптимальних рішень, називаються правилами відсіву.
У даний час найбільш широко вживаними є три групи методів:
• методи локальної оптимізації;
• методи випадкового пошуку;
• методи розгалуження.
Розглянемо коротко суть цих методів.
При локальній оптимізації для кожної комбінації pi ∈ P визначається Qi – множина комбінацій, сусідніх із pi. Вихідною операцією є випадковий вибір початкової комбінації. Потім на множині Qi знаходять локальний екстремум. Цей процес повторюється багато разів, і серед отриманих локальних екстремумів вибирається найменший, і саме він приймається за наближене значення.
При випадковому пошуку вибір всіх комбінацій відбувається випадково, відповідно до деякого закону розподілу. Значення цільової функції на цих комбінаціях обчислюються, і серед них вибирається та комбінація, яка дає екстремальне значення цільової функції. Основною проблемою при випадковому пошуку є вибір істотних ознак комбінацій. Тут найпопулярнішими є два підходи:
• ознаки вибирають заздалегідь шляхом аналізу умов задачі;
• ознаки отримують з аналізу вже отриманих рішень.
Методи розгалуження. Вперше метод гілок і меж був запропонований для розв’язку задач цілочислового лінійного програмування.
Надалі цей метод був застосований до загальніших класів комбінаторних оптимізаційних задач. За способом розгалуження всі алгоритми гілок і меж можна розділити на такі групи:
1. Алгоритми, що будують дерево підзадач вихідної задачі (наприклад, алгоритм Ленд і Дойга, запропонований для розв’язку задач цілочислового програмування. У цьому методі будується дерево задач лінійного програмування, домагаючись поступового задоволення умов цілочисловості – варіант методу відсікань);
2. Алгоритми, що будують дерево неприпустимих рішень (наприклад, адитивний алгоритм Балаша і його модифікації). Цей метод застосовується для розв'язання задач лінійного програмування з булевими змінними;
3. Алгоритми, що будують дерево допустимих рішень (наприклад, метод вирішення задач про комівояжера).
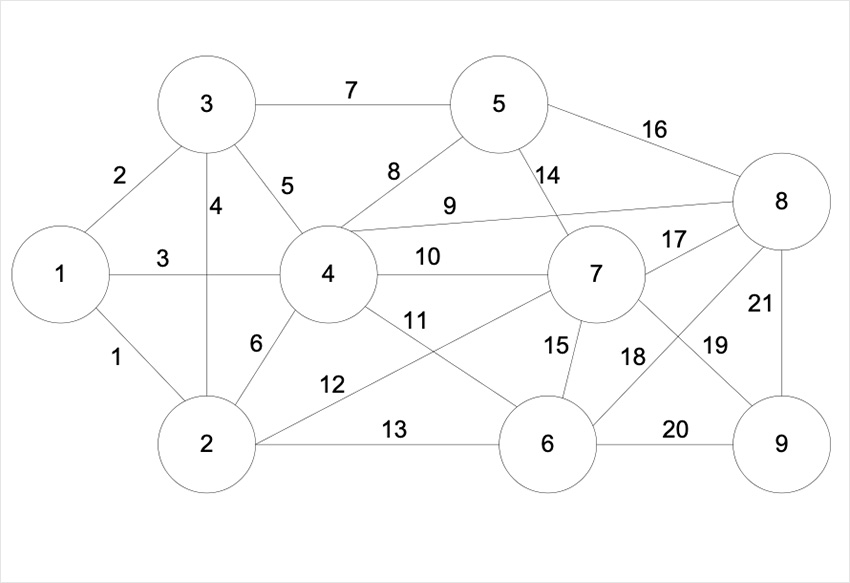
Для прикладу, зважаючи на велику популярність і поширеність задачі про комівояжера, опишемо послідовність дій (алгоритм) у методі гілок і меж для цієї задачі:
1) вибирається деяка повна гілка, і обчислюється довжина маршруту; цю гілку називають еталонною;
2) розглядаються інші початкові ділянки маршруту; для кожного з них послідовно обчислюються оптимістичні оцінки нижньої межі довжини маршруту;
3) порівнюється оцінка чергової ділянки маршруту з довжиною еталонної гілки:
- якщо оптимістична оцінка більша від довжини еталонної гілки, то ділянка – безперспективна, і далі розгалуження робити не потрібно,
- інакше, з кінцевої вершини ділянки здійснюється розгалуження, тобто перебір ділянок, що містять на одну вершину більше, ніж розглянута ділянка.
Процес триває до отримання повної послідовності.
Якщо довжина маршруту, що відповідає еталонній послідовності, менша за довжину еталонної гілки, то її вважають еталонною.
Остання еталонна послідовність буде оптимальною.
У даний час сформульовано велику кількість оптимізаційних комбінаторних задач, що мають широке практичне використання. З огляду на їхню популярність, перерахуємо лише назви (за назвою приблизно можна уявити зміст задачі) деяких з них, не вдаючись до їхнього змісту:
• задача про ранець;
• задача про комівояжера;
• задача мінімізації середнього часу обробки партії деталей;
• задача про призначення;
• задача про покриття;
• задача компонування
та інші.
Розроблено також цілу низку комбінаторних методів. Знову перерахуємо тільки назви тих методів, які найчастіше застосовуються при розв’язку наведених задач:
• метод послідовного аналізу варіантів;
• метод гілок і меж;
• локальні алгоритми;
• методи, засновані на послідовних схемах;
• метод динамічного програмування;
• апроксимаційно-комбінаторний метод.
Відзначимо, що всі наведені методи є універсальними, і саме їхня універсальність обумовлює надзвичайну широту їхнього застосування до конкретних задач.
На основі цих методів іноді розробляються гібридні методи.
3. Наближені методи. Ці методи широко застосовуються при розв’язку задач з наближеним рішенням, оскільки знаходження точного рішення може вимагати значних обчислювальних ресурсів. Сучасні наближені методи, зазвичай, є комбінованими, тобто містять у собі елементи різних методів. У наближених методах рішення задачі проводиться, переважно, у два етапи: побудова початкового рішення і уточнення початкового рішення.
При цьому на першому етапі широко використовуються евристичні алгоритми – алгоритми, засновані на правдоподібних, але не обґрунтованих строго припущеннях про властивості оптимального рішення задачі.
Прикладом евристичного алгоритму може бути алгоритм розв’язку задачі комівояжера, в якому на кожному кроці реалізується перехід в найближчу із залишених точок. Алгоритми такого типу носять назву «greedy» («жадібні» алгоритми чи алгоритми, які пожирають «машинний» час).
Ці алгоритми на кожному кроці розв’язують «локальну» задачу оптимізації; проте отримане рішення може бути як завгодно далеким від оптимуму.
На другому етапі використовуються алгоритми локальної оптимізації, пов'язані з введенням поняття околиці; при цьому можна використовувати різні алгоритми цього типу, змінюючи правила вибору околиці.
В основному, наближені методи базуються на відмові від пошуку точного рішення і введенні замість цього додаткової умови припинення процесу оптимізації.
Наприклад, замість пошуку x ∈ M, для якого f(x) є мінімальною, ставиться задача пошуку такого x* ∈ M, що f(x0) - f(x*) < ε або (f(x0) - f(x*)) / f(x*) < ε, ε > 0, тобто фактично умови подібного роду вимагають пошуку лише точок, в яких функція істотно зменшується, але мінімуму може і не досягати.
Підставою для переходу до наближених методів є такі ознаки задачі:
• експонентне (дуже швидке) зростання обсягу обчислень з ростом розмірності задачі; це явище отримало назву «прокляття розмірності»;
• для точного розв'язання задач великої розмірності потрібні потужні комп'ютери, а наближені рішення можна отримати на наявних комп’ютерах;
• у прикладних задачах, як уже зазначалося, часто вихідну задачу вдається сформулювати лише приблизно, тоді точне рішення не має сенсу і може мати скоріше теоретичний інтерес;
• вихідні дані в прикладній задачі відомі, зазвичай, приблизно, відповідно, наближеними є і параметри моделі, тому пошук точного рішення є невиправданим.
Від наближених методів, що гарантують пошук рішення із заданою точністю, слід відрізняти різного роду «евристичні» методи, які таких властивостей одержуваних рішень не гарантують. Їхнє використання виправдане тільки при повній відсутності інших можливостей. Відзначимо також, що існують задачі, в яких потрібні саме точні рішення, наприклад, потрібно дати конкретну відповідь: «так» чи «ні».
А.О. Антонюк, кандидат фізико-математичних наук
















 Засновник та видавець
Засновник та видавець