Вступ
Нарди є цікавою стародавньою грою, історія якої налічує близько 5 тисяч років. Ця гра відноситься до так званих комерційних ігор, де успіх залежить як від везіння, так і від навичок гравців. Нині спостерігається підвищення інтересу до цієї гри у всьому світі. В першу чергу цьому сприяє комп'ютеризація. З одного боку, у гравців з’явилась можливість грати через мережу інтернет з суперниками, що знаходяться в будь-якій точці земної кулі. З іншого боку, з’явилися програми, здібні аналізувати та порівнювати різні позиції, давати гравцю поради та робити зауваження, щодо його гри. Слід також відзначити активне втручання математики в нарди, насамперед таких її розділів, як теорія ймовірностей та теорія ігор.

(Манесський рукопис, Великий
Гайдельберзький рукопис) – найбільш
відомий середньовічний ілюстрований
пісенник німецькою мовою
Правила гри
Наведемо правила двох найбільш розповсюджених варіантів гри в нарди – довгі та короткі. Спочатку розглянемо правила, спільні для двох варіантів.
Гральна дошка складається з 24 полів та поділена на 4 чверті (або квадранти), по 6 полів в кожній чверті. Кожний з гравців грає 15 шашками.
Право першого ходу визначається жеребкуванням. Гравці кидають по одному кубіку. Якщо на кубіках випадають однакові цифри, то гравці кидають кубики ще раз доти, доки не випадуть різні числа. Гравець, який викинув більше число, виграє право першого ходу. За одним варіантом попередньої домовленості вважається, що першим кидком гравця є числа, викинуті в результаті жеребкування. За іншою домовленістю гравець, що виграв жеребкування, кидає два кубіки,
Далі гравці по черзі кидають на дошку 2 кубики і пересувають шашки в заданому правилами гри напрямку згідно цифр, що випали на кубиках. Наприклад, нехай випало 5-3. Гравець, який викинув таку комбінацію, повинен деяку шашку пересунути на 5 полів, а деяку – на 3. Якщо гравець пересунув шашку на 5 полів, то кажуть, що він зіграв 5. Яку з двох цифр зіграти спочатку, а яку потім, гравець вибирає на свій розсуд.

манускрипті The Luttrell Psalter,
створеному невідомими авторами
в 1320 – 1340 роках, є зображення
короля і дами, які грають в настільну гру,
що дуже нагадує нарди
Дубль. Якщо гравець викинув однакові цифри на обох кубиках (наприклад, 4-4), то кажуть, що він викинув дубль, або куш. Тоді його хід подвоюється, тобто він повинен зіграти викинуте число не 2, а 4 рази.
В процесі гри гравець може блокувати певні поля своїми шашками. Це означає, що його противнику заборонено ставити свої шашки на ці поля. В довгих та коротких нардах блокування полів здійснюється зовсім різним чином (як саме- буде розглянуто надалі). Оскільки деякі поля можуть бути заблоко-ваними, то в обох варіантах гри може виникнути ситуація, в якій гравець не може зіграти викинуті числа, або зіграти частково. Такі ситуації регламентуються наступними правилами.
1) Якщо гравець якимось чином може зіграти два викинутих числа, то він повинен це зробити, якщо навіть це призводить до поганої для нього позиції.
2) Якщо в ніякому разі не можна зіграти два викинутих числа, грається те число, яке можна зіграти. При цьому, якщо розігрування одного числа блокує можливість зіграти інше, то гравець повинен зіграти більше з викинутих чисел.

голландський живописець і графік
3) Якщо не можна зіграти жодного з викинутих чисел, то гравець не персуває шашки, і хід, як зазвичай, переходить до суперника.
Метою гри є перенести всі шашки в квадрант, який називається дім, після чого починається викидання шашок з дому, (процедура викидання шашок аналогічна в обох варіантах гри). Викидання можна здіснювати лише тоді, коли всі шашки зібрано в домі. Гравець, який викинув всі шашки зі свого дому раніше, ніж противник, виграє.
Нарахування виграшу. Гравець, який викинув з дому всі шашки раніше противника, виграє одне очко. Якщо гравець викинув всі свої шашки, а його противник жодної, то гравець виграє два очки (така ситуація називається марс, англійською мовою – gammon).
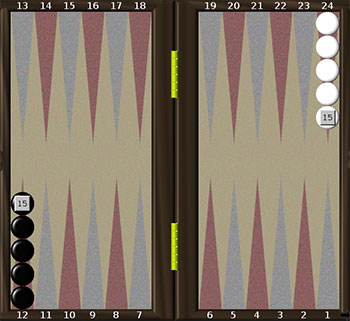
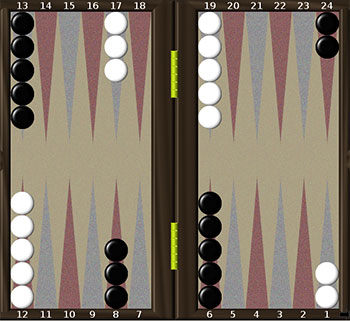
Довгі нарди
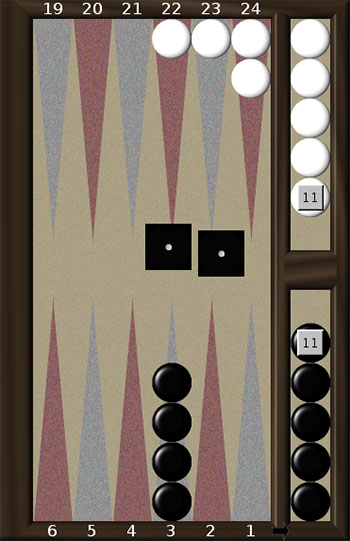
Початкове розміщення шашок показано на рис. 1а. З самого початку у кожного з гравців всі 15 шашок знаходяться на лівому нижньому полі і називаються головою або стеком. За один хід з голови можна пересувати не більш, ніж одну шашку. Вийнятком цього правила є ситуація, коли в першому ході гравця випадає дубль – тоді з голови дозволяється зіграти дві шашки. Обидва гравці пересувають свої шашки проти годинникової стрілки. Метою білих є завести всі шашки в свій дім (поля 1-6) і потім викинути їх з дому. Чорні мають аналогічну мету, але їхній дім – це поля 13-18. Гравець може пересувати свої шашки на вільні поля та на поля, на яких вже знаходяться його інші шашки. Поле, на якому є принаймні одна шашка гравця є заблокованим для його противника, тобто ставити на нього шашки заборонено.
Короткі нарди
Початкове розміщення шашок показано на рис. 1 б. Чорні пересувають шашки проти годинникової стрілки, та їхнім домом вважаються поля 1-6. Білі пересувають свої шашки за годинниковою стрілкою та їхнім домом є поля 19-24. Таким чином, на самому початку грі гравці вже мають по 5 шашок у своєму домі. На відміну від довгих нард, заблокованим для противника є поле, на якому стоять дві або більше шашок гравця. Поле, на якому стоїть одна шашка противника, можна займати, вибиваючи її. При цьому вибита шашка ставиться “на борт” в середню частину дошки. Гравець, який має вибиту шашку, повинен під час свого ходу знову ввести її у гру, і поставити її в дім противника в одну з позицій, номер якої відповідає цифрі, що випала на одному з кубиків (це називається “зарядитись”). Якщо відповідні поля вже зайняті противником, то шашка лишається на борту, і гравець втрачає хід. Гравець не може пересувати інші шашки доти, доки не зарядить всі вибиті.
Викидання шашок з дому
Викидання шашок є останнім етапом гри та є аналогічним в обох варіантах (тільки в коротких нардах дома противників знаходяться один навпроти одного, а довгих – по діагоналі). Нагадаємо, що викидання можна розпочати лише після того, як всі шашки було заведено в дім. Кожну цифру, що випала на кубиках, гравець на свій розсуд може зіграти, викинувши шашку, що стоїть у позиції з відповідним номером або “переграти”, тобто пересунути деяку шашку так, що номер її позиції зменшиться на число, яке випало.
Якщо на шостому полі вже немає шашок, а випадає цифра 6, то гравець повинен викинути шашку з поля з найбільшим номером. Якщо вільні 6 та 5 поля то гравець у випадку, якщо випадає 5 або 6, знімає шашку з 4-го поля і т.д. Наприклад, в позиції 2в. кидок 6-5 грається 4-Off,3-Off.
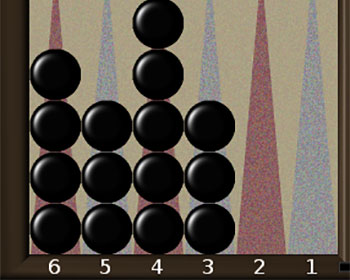
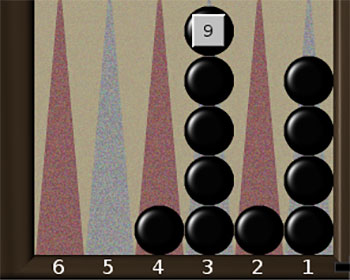
Розглянемо позицію 2 а. 6-ку можна зіграти єдиним чином – викинути шашку з 6-го поля (6-Off), 5-ку – двома шляхами – 5-Off або 6-1, 2-ку зняти не можна, але можна переграти різними шляхами – 6-4, 5-3, 4-2 або 3-1. Нехай випало 5-5. Це дуже вдалий кидок, найкращий спосіб його зіграти –це 5-Off (3 рази), 6-1. Нехай випало 6-6 – це найкращий кидок. Його можна зіграти лише одним способом – 6-Off (4-рази). Після цього шосте поле стає вільним. Нехай наступний кидок був 6-4. Його можна зіграти двома способами – 5-Off, 4-Off, або 5-Off,5-1, кращим є перший спосіб.
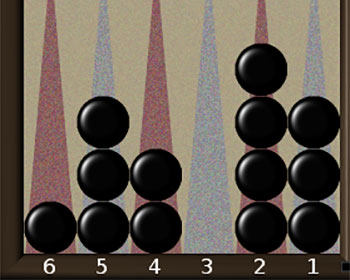
Розглянемо позицію 2б. Нехай випало 3-3. 2 трійки можна використати на 6-Off, дві інші трійки гравець вимушений перегравати (найкращий спосіб- 5-2 (2 рази). Нехай випало 6-3. Тут не треба спішити викидати 6-Off та перегравати 5-2 або 4-1. Краще спочатку переграти 6-3, тоді шосте поле стає вільним і 6-ку можна зіграти 5-Off. Цей прийом називається “заповнення щілини”. Якщо в одному з наступних кидків випаде 3-ка, то можна буде викинути шашку, замість того, щоб лише перегравати.
Вважається, що при викиданні шашок знайти найкращу гру допомагає “жадібний принцип”- викидати якомога більше шашок, і перегравати лише тоді, коли викидати неможливо. Наприклад, в позиції 2 б. кидок 4-2 треба грати 4-Off, 2-Off (хоча, можливо, хочеться переграти 2-ку 5-3, щоб закрити щілину). Дубль 2-2 слід грати 2-Off (4 рази) і т.д. Як показало комп’ютерне моделювання, даний принцип є справедливим у значній більшості випадків, але можуть бути і вийнятки. Ситуації, в яких правило працює завжди, такі. Залишити на дошці одну шашку завжди краще, ніж дві, а дві- краще, ніж три. Розібраний далі приклад (6 б). є контрприкладом, щодо жадібного правила, який показує, що іноді залишити чотири шашки краще, ніж три.
Позиція 2в є ще одним контрприкладом, щодо жадібного принципу. Нехай випало 2-4. Виявляється, що гра 4-2, 3-Off при будь-якій позиції противника є не гіршою (а іноді кращою), ніж 4-Off, 2-Off (читачеві пропонується подумати, чому саме).
Надалі ми знайдемо оптимальні ходи для випадку, коли на дошці лишається лише дві шашки. Але для цього треба буде розібратись, що таке класична формула ймовірності.
Класична формула ймовірності
Нехай множину всіх можливих випадкових подій можна представити як сукупність елементарних подій, Нехай при цьому елементарні події мають такі три властивості
- Події є взаємно виключними (тобто, якщо в результаті випробування відбувається одна з подій, то це виключає реалізацію будь-якої іншої події).
- Події утворюють повну групу подій (тобто завжди в результаті випробування відбувається одна з подій).
- Події є рівноймовірними (тобто, ймовірності реалізації всіх елементарних подій однакова. Якщо повна група подій складається з n елементарних подій, то ймовірність реалізації кожної елементарної події дорівнює 1/n.
Тоді, ймовірність реалізації деякої складної події А є відношення кількості елементарних подій, що є сприятливими для А до загальної кількості елементарних подій.
Пояснимо дану формулу на прикладах. Нехай підкидається гральний кубік, на гранях якого нанесені числа від 1 до 6. Тоді множина елементарних подій є множина цілих чисел від 1 до 6: {12,3,4,5,6}. При цьому ця множина подій задовольняє переліченим трьом властивостям.
По-перше, два числа не можуть випасти одночасно, отже події є взамовиключними.
По-друге, кубик є “правильною” геометричною фігурою, і кожна з його граней не відрізняється від інших, отже ймовірності випадіння чисел від 1 до 6 однакові і дорівнюють 1/6.
По-третє, множина чисел {12,3,4,5,6} утворює повну групу подій, оскільки в результаті підкиданні кубика завжди випаде якесь з цих чисел.
Знайдемо ймовірності деяких складних подій.
Задача. Знайти ймовірність того, що на гральному кубику випаде непарне число.
Розв’язок. Всього на кубику 6 чисел, з них непарними є 1, 3 та 5 (разом 3 числа). Отже, шукана ймовірність дорівнює 3/6=1/2.
Задача. Знайти ймовірність того, що на гральному кубіку випаде число, яке є квадратом цілого числа.
Розв’язок. Всього на кубику 6 чисел, з них квадратами є 1 та 4 (разом 2 числа). Отже, шукана ймовірність дорівнює 2/6=1/3.
Нехай тепер одночасно підкидається два кубики. Пофарбуємо кубики в різні кольори для того, щоб їх можна було б відрізняти один від одного. Тоді множина елементарних подій – це множина впорядкованих пар (i,j), де i та j – це цифри, що випали на першому та другому кубиках відповідно (звичайно, це цілі числа від 1 до 6). Тут принциповим є те, що пара є впорядкованою, тобто наприклад (2,5) та (5,2) – це дві різні події. Тоді загальна кількість елементарних подій дорівнює 6·6=36. При цьому зрозуміло, що всі 36 елементарних подій є взаємно виключними, рівноймовірними та утворюють повну групу подій.
Тепер можна забути про фарбування кубиків (зазвичай, гравці підкидають два кубики, які не можна відрізнити один від одного, але треба пам’ятати, що комбінації з двома різними цифрами (наприклад, 1-2) відповідає дві елементарні події, а комбінації з однаковими цифрами (наприклад 1-1) – лише одна.
Задача. Знайти ймовірність того, що сума очок на двух кубиках дорівнює 6.
Розв’язок. Для цієї події сприятливими є такі комбінації: 1-5, 2-4 та 3-3. При цьому, комбінації 1-5 та 2-4 треба рахувати двічі, а 3-3 – лише один раз, отже, кількість сприятливих подій дорівнює 5. Отже, шукана ймовірність дорівнює 5/36.
Задача. Знайти ймовірність того, що при підкиданні двох кубиків випаде така комбінація, в якій одне з чисел ділиться не друге.
Розвязок. Складемо таблицю, в якій сприятливі комбінації будемо позначати +, а несриятливі –.
Табл. 1.
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | + | + | + | + | + | + |
| 2 | + | + | - | + | - | + |
| 3 | + | - | + | - | - | + |
| 4 | + | + | - | + | - | - |
| 5 | + | - | - | - | + | - |
| 6 | + | + | + | - | - | + |
В таблиці 1 є 22 плюси, отже, ймовірність дорівнює 22/36=11/18.
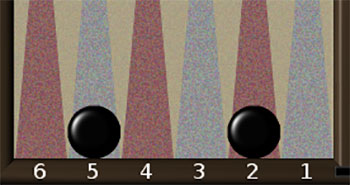
Застосуємо метод складання таблиць для аналізу передостаннього ходу в нардах.
Нехай у гравця в домі залишилась одна шашка на 2 та одна на 5. Яка ймовірність того, що він викине обидві шашки за один хід?
Знову малюємо таблицю 6×6. Сприятливими є комбінації, в яких менше число не менш, ніж 2, а більше – не менш – ніж 5. Крім того, не забуваємо, що дублі 2-2 та 3-3 також є сприятливими, оскільки гравець має 4 ходи. Наприклад, в результаті розіграшу комбінації 2-2 маємо:
2-Off (що означає викидання), 5-3, 3-1, 1-Off.
Табл. 2.
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | - | - | - | - | - | - |
| 2 | - | + | - | - | + | + |
| 3 | - | - | + | - | + | + |
| 4 | - | - | - | + | + | + |
| 5 | - | + | + | + | + | + |
| 6 | - | + | + | + | + | + |
В таблиці 2 є 19 плюсів, отже, шукана ймовірність дорівнює 19/36.
Аналогічним чином, обчислимо ймовірності викидання для всіх можливих випадків з однією та двома шашками (читачеві пропонується зробити це самостійно, хоча б для декількох варіантів). Наведені числа – це шанси закінчити гру на даному ході (з 36).
Одна шашка. В першому рядку наводиться позиція шашки (від 1 до 6), в другому – кількість шансів її викинути (з 36).
Табл. 3.
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| 36 | 36 | 36 | 34 | 31 | 27 |
Дві шашки. Для всіх можливих варіантів розташування двох шашок обчислено ймовірність викинути обидві шашки за один хід.
Табл. 4.
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 36 | 36 | 34 | 29 | 23 | 15 |
| 2 | 36 | 26 | 25 | 23 | 19 | 13 |
| 3 | 34 | 25 | 17 | 17 | 14 | 10 |
| 4 | 29 | 23 | 17 | 11 | 10 | 8 |
| 5 | 23 | 19 | 14 | 10 | 6 | 6 |
| 6 | 15 | 13 | 10 | 8 | 6 | 4 |
Покажемо, як дані таблиці можуть бути корисними для вибору найкращого ходу.
Розглянемо позицію (рис. 3а). Чорні викинули 6-1. Нажаль, цього недостатньо, щоб викинути всі три шашки (достаньою є лише одна комбінація 6-6). Чорні сподіваються, що білі не викинуть свої шашки, і чорні зможуть виграти на своєму наступному ході. Звичайно, чорні викидають шашку з 6 (6-Off). Як зіграти 1 – пересунути (“переграти”)
шашку з 6 на 5, або з 3 на 2? В результаті залишаються позиції двох шашок 5-3 та 6-2 відповідно. З таблиці 4 знаходимо, що комбінація шашок 5-3 дає 14 шансів а 6-2 –лише 13. Отже, 5-3 є кращою, і кращим ходом є 6-Off, 6-5.
Розглянемо позицію (рис. 3б). Чорні викинули 5-2. Звичайно, треба викинути 5 (5-Off). Як зіграти 2 – з 6 на 4 чи з 3 на 1? В результаті отримаємо комбінації двох шашок 4-3 та 6-1 відповідно. З таблиці 4 знаходимо, що комбінація 4-3 (17 шансів) є кращою, ніж 6-1 (15 шансів).
Розглянемо позицію 3 в). На перший погляд здається, що 4-2 –це дуже поганий кидок – треба переграти 5-1 та 3-1. В результаті в чорних залишається 3 шашки на одиниці, і навіть якщо чорні матимуть можливість наступного ходу, то сприятливими кидками будуть лише дублі (всього 6 комбінацій). Але подивимось уважніше. Як відмічалося раніше, кидок можна розігрувати у будь-якій послідовності. Спочатку зіграємо двійку – переграємо 5-3. Таким чином, на позиціях 4, 5 та 6 не залишилось шашок. Тепер четвірку можна використати на те, щоб викинути шашку з трійки 3-Off. В результаті залишиться позиція 3-1. Якщо чорні матимуть можливість наступного ходу, то викинуть свої дві шашки з ймовірністю (лише комбінація 1-2 буде несприятливою).
Звернемо увагу на те, що для того, щоб правильно розігрувати передостанній хід, не обов’язково вчити напам'ять таблицю 4. Зробимо з неї лише потрібні корисні витяжки. Гравець вибирає, яку з двох шашок, що лишились, треба переграти, але в будь якому разі сума позицій шашок, що лишилися, залишається незмінною (в прикладі 1а) гравець вибирає між позиціями 5-3 та 6-2, 5+3=6+2=8. Порівняємо різні позиції при фіксованій сумі. Так, наприклад, для суми 7 матимемо, що позиція 2-5 (19 шансів) є кращою, ніж 3-4 (17 шансів), яка в свою чергу є кращою, ніж
1-6 (15 шансів). Висновки для різних сум представимо у вигляді таблиці 5.
Табл. 5.
| (1-3) > (2-2) |
| (1-4) > (2-3) |
| (1-5) = (2-4) > (3-3) |
| (2-5) > (3-4) > (1-6) |
| (3-5) > (2-6) > (4-4) |
| (3-6) = (4-5) |
| (4-6) > (5,5) |
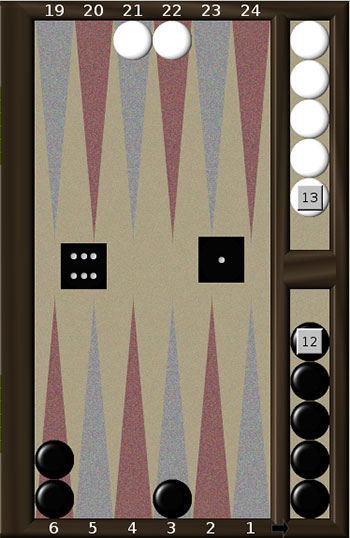
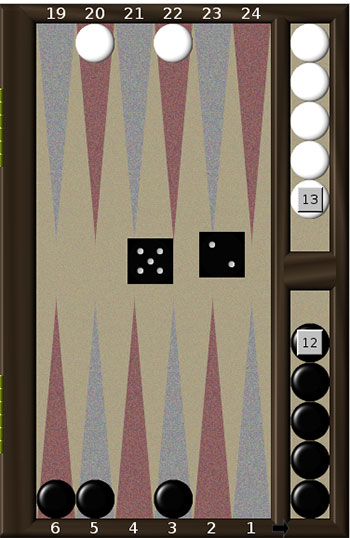
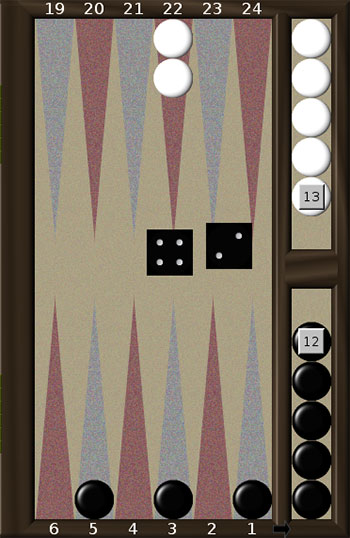
Навіть наприкінці гри для вибору найкращого ходу треба враховувати не тільки свою позицію, а й позицію противника.
Продемонструємо технічний прийом, який носить назву “підготовка дубля”.

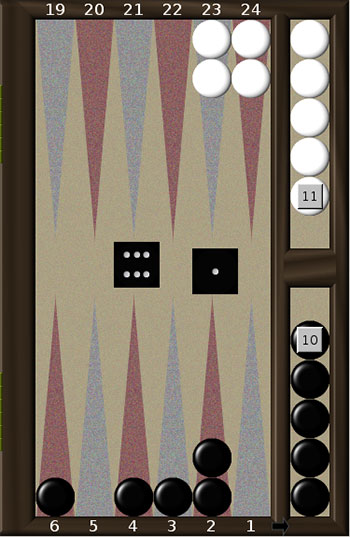
Порівняємо позиції, представлені на рис. 4 а. та 4 б. Нехай чорні мають зіграти 1-6. Суто зовнішнє вони відрізняються лише тим, що в позиції 4а. у білих в на одну шашку більше. Але це міняє стратегію гри чорних. В позиції 4а. правильним ходом чорних є 6-Off, 2-1. В результаті чорні матимуть 4 шашки на полях 4, 3, 2 та 1. Скоріш за все (якщо білі не викинуть дубль) у білих буде ще два ходи, і за два ходи чорні мають гарніі шанси викинути свої чотири шашки.
В позиції 4б. справи чорних значно гірші. В найкращому для них випадку (якщо білі не викинуть дубль), в них залишиться лише один хід. Зняти чотири шашки, що лишились, можна лише якщо викинути дубль. Подивимось, які саме дублі будуть сприятливими. Якщо, як і в попередньому прикладі, зіграти 6-Off, 2-1, то сприятливими будуть дублі
6-6, 5-5 та 4-4. Але якщо зіграти 6-Off, 4-3 (що на перший погляд здається нелогічним), то сприятливим стає також дубль 3-3 (кажуть, що гравець підготував 3-3).
Третій можливий хід 6-Off, 3-2 не є кращим в обох позиціях. Наведемо ймовірності у відсотках виграшу чорних, розраховані програмою Gnu backgammon.
Табл. 6.
| 2а | 2б | |
|---|---|---|
| 2а | 2б | |
| 6-Off, 2-1 | 62,93 | 7,18 |
| 6-Off, 4-3 | 44,07 | 9,57 |
| 6-Off, 3-2 | 43,00 | 7,18 |
Наведемо інші приклади підготовки дубля.
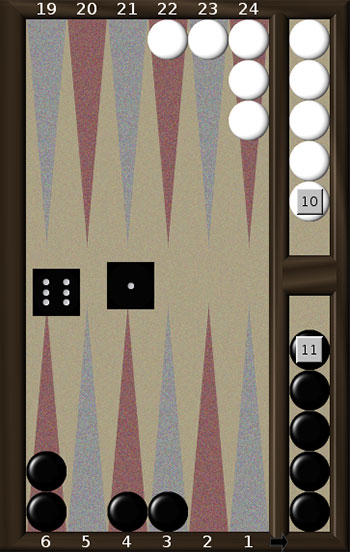
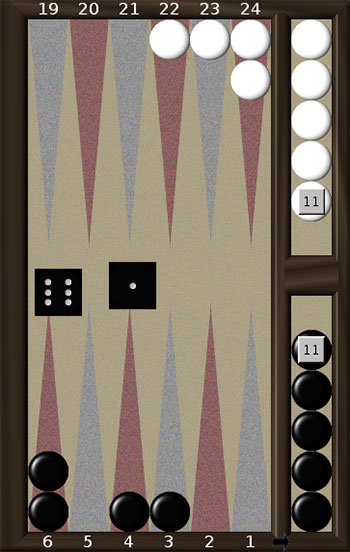
В ситуації на рис. 5а. чорні після свого ходу скоріш за все матимуть ще два ходи. Гра 6-Off, 6-5 залишає три шашки на полях 5, 4, 3, що дає непогані шанси викинути їх за наступні два ходи (якщо за перший хід вдається зняти лише одну шашку, то ми вже знаємо, як переграти другу. Наприклад, кидок 5-2 треба грати 5-Off, 3-1,що є кращим, ніж 5-Off, 4-2).
В позиції 5б. скоріш за все у чорних буде лише ще один хід. Тому нелогічна на перший погляд гра 6-Off, 4-3 додає дубль 3-3 до множини сприятливих кидків (6-6, 5-5 та 4-4 є сприятливими у будь-якому разі).
Гра 6-Off, 4-2 не є оптимальною в будь-якому разі.
Результати комп’ютерних розрахунків наведено в таблиці 7
Табл. 7.
| 2а | 2б | |
|---|---|---|
| 6-Off, 6-5 | 55.48 | 7,62 |
| 6-Off, 4-3 | 52.12 | 10.06 |
| 6-Off, 3-2 | 55.37 | 7,62 |
Аналогічно, в ситуації 6а. найкращою грою є 3-Off, 3-1, у той час як у 6б. найкращою грою, що готує дубль 2-2 для наступного ходу, є 3-2 (4 рази).

Висновки
Розібрані приклади показують, що виграш залежить як від везіння, так і від вміння гравців. Звичайно, кожен гравець сподівається на везіння. Але для того, щоб фортуна посміхалася якомога частіше, треба зі свого боку робити правильні ходи в кожному випадку надавати їй якомога більше можливостей посміхатись саме вам.
С.І. Доценко, кандидат фізмат наук, доцент факультету інформаційних технологій КНУ ім. Тараса Шевченка




















 Засновник та видавець
Засновник та видавець