Злом коду Енігма
Одним з ключових завдань, поставлених британською розвідкою, було перехоплення і розшифровка повідомлень, переданих німецькими військами. Треба віддати належне, німецькі шифри були дуже хороші, проте вони були зламані зусиллями групи британських учених. Ось деякі деталі цієї історії.
Для передачі і прийому повідомлень німецькими військами використовувалася шифрувальна машина «Енігма», що зовні нагадує друкарську машинку. У Блечлі-парку недалеко від Лондона для розшифровки коду було створено таємну лабораторію, в якій була зібрана група фахівців із криптографії. Найвідомішим із них був англійський математик Алан Тьюрінг, який виконав теоретичну частину роботи, пов'язану з криптографічним аналізом.
Але як вдавалося зламувати настільки складний шифр, адже він змінювався німцями щоночі? У шифрувальній машині був помічений такий недолік, що кожна буква ніколи не залишалася в підстановлюваному шифрі на своєму місці, тобто замість А ніколи не підставлялась А і т.д.
Дослідницька група мала у своєму розпорядженні зразок машини «Енігма», і на її основі була сконструйована дешифрувальна машина «Бомба», що повторювала з'єднані разом кілька десятків машин «Енігма».
Першим повідомленням, яке німці передавали протягом дня, був прогноз погоди, і це служило одним із ключів до розгадки, оскільки було відомо, який приблизно прогноз на поточний день і які ключові слова будуть вживатися в цьому повідомленні. На розгадку шифру, актуального протягом дня, йшло близько 20 хвилин.
Після закінчення Другої світової війни Черчилль з міркувань секретності наказав знищити всі матеріальні сліди програми досліджень, зокрема і «бомбу». Але згодом британські любителі історії за кресленнями відтворили машину, яка зберігається в музеї Блечлі-парку.
Ті, хто зацікавився даною історією, можуть подивитися документальні фільми «Людина, яка зламала код нацистів» і «Алан Тьюрінг. Він обганяє час» (є на Youtube), а також художні фільми «Код Енігма» (2001 р.) і «Гра в імітацію» (2014 р.).
Задача про німецькі танки
Під час Другої світової війни обсяги випуску німецьких танків, наприклад марки «Пантера», були оцінені з високою точністю за допомогою статистичних методів, і як виявилося згодом, дані статистичних оцінок були набагато ефективнішими, ніж дані розвідки.
Наведемо коротко суть статистичного методу оцінки.
Виявилося, що на всіх випущених танках ставилися місяць випуску і серійні номери, причому кожен місяць нумерація знову починалася з одиниці. Якщо танк опинявся підбитим у ході військових дій, то його номер, серійний номер і місяць випуску ставали відомими.
Виявляється, що корисну інформацію для статистичного аналізу несуть тільки два показники - кількість номерів і максимальне значення.
Можна легко вирішити таку ймовірнісну задачу. Якщо з набору чисел від 1 до n зроблена випадкова вибірка без повторення k чисел, то ймовірність того, що максимальним у цій вибірці буде m, дорівнює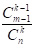 
.
Наприклад, ймовірність того, що в лотереї «5 з 36» максимальним номером буде 25, дорівнює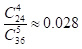 
. Це легко пояснити.
Всього k чисел з n можна вибрати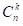 
способами. Порахуємо кількість способів, при яких максимальне число з k вибраних дорівнюватиме m (де k≤m≤n). При цьому одне число з k потрібно зафіксувати в позиції m, а решта k-1 чисел можуть приймати будь-які значення від 1 до m-1, і таким чином шукане число способів дорівнює 
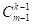, а шукана ймовірність – 
.
Але повернемося до оцінки кількості випущених танків. На жаль, ця задача є оберненою до розглянутої нами - ми навчилися будувати ймовірнісний розподіл m при відомому n, а потрібно навпаки.
Виявляється, що такий імовірнісний розподіл теж можна побудувати, і на допомогу приходить формула Байєса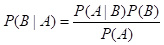 
.
Задача про бомбардування Лондона
З червня по жовтень 1944 року фашистська Німеччина випустила в бік Англії 9.5 тисяч самохідних літаючих бомб, з яких 2.4 тисячі впали на Лондон.
Британці сильно переживали і задавалися питанням - чи падали бомби на місто випадковим чином, чи вражали намічені цілі? Допомогти відповісти на це питання зміг метод, розроблений видатним англійським математиком і статистиком Карлом (Чарльзом) Пірсоном і який називається критерій Пірсона або хі-квадрат критерій.
Територія міста була умовно розбита на 24 × 24 = 576 квадратних ділянок, і були зібрані і оброблені дані про розподіл кількості бомб, які потрапили на ці ділянки.
| Кількість попадань | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Кількість ділянок | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Якщо бомбардування проводилося б хаотично, то отримані статистичні дані про розподіл числа влучень повинні були б узгоджуватися з розподілом Пуассона (про який буде стаття в одному з наступних випусків).
Виявилося, що згідно з критерієм Пірсона дані про бомбардування добре узгоджуються з розподілом Пуассона, і був зроблений висновок, що бомбардування носить хаотичний характер.
Задача про аналіз крові
Видатний американський математик і економіст Роберт Дорфман під час Другої світової служив у військово-повітряних силах США.
При проходженні новобранцями медичної комісії повинні були обов'язково здаватися аналізи крові на тест Вассермана. Це якісний аналіз, який показує, що людина хвора, якщо в її крові є певні антитіла. Для здачі тесту усіма призовниками виникала потреба у великій кількості тестових препаратів і потрібно було мати багато часу на проведення тестування.
І тоді Дорфман запропонував просту і геніальну ідею, що дозволяє істотно скоротити кількість проведених аналізів.
Оскільки позитивний тест реакції Вассермана зустрічається нечасто, то потрібно змішати зразки крові декількох (k) призовників і провести тест суміші. Якщо результат такого тесту негативний, то це означає, що результат для кожного з тестованих також негативний, і, таким чином, у цьому випадку був проведений всього один тест замість k, отже, зекономлено k-1 тестів.
Якщо ж тест позитивний, хворий один або кілька людей з k, і далі вони проходять індивідуальні тести, і це означає, що був зроблений один зайвий тест.
Таким чином, виникає питання, як вибрати оптимальний розмір групи тестованих, адже, з одного боку, з ростом k зростає кількість зекономлених тестів у разі негативного результату, з іншого боку, зростає ймовірність позитивного результату (в результаті чого буде витрачено додатковий тест).
Знайдемо оптимальне значення k. Нехай p - ймовірність позитивного результату тесту у одного призовника (цю величину легко оцінити як частоту, обчислену за сукупністю вже досліджених призовників).
Тоді тест суміші з k зразків дасть негативний результат з імовірністю (1-p)k і позитивний з додатковою можливістю, тоді в середньому знадобиться
(1-p)k +(k+1)(1-(1-p)k)=(k+1)-k(1-p)k
тестів, що в перерахунку на одного призовника складе
.
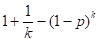Замінимо k дійсною величиною x і будемо шукати точку максимуму функції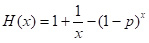 
.
Мінімум H (x) досягається в точці x0, де x0 - менший корінь рівняння H'(x) = 0, тобто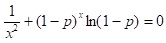 
.
Якщо p мале (а в реальній ситуації так і було), то рівняння можна спростити, поклавши (1-p)x≈1-px, ln(1-p) ≈-p, тоді отримуємо рівняння
,
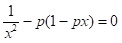корінь якого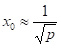 
, тоді
.
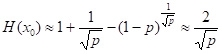Наприклад, при p=0,01 беремо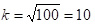 
, H(x) ≈ 0,2. Це означає, що кількість проведених тестів зменшиться у 5 разів!
С.І. Доценко, канд. фізмат наук, доцент факультету інформаційних технологій, КНУ імені Тараса Шевченка
Засновник та видавець