Думаю, що таке викладення може продемонструвати школяреві наочний, не надуманий приклад введення математиками абстрактних понять, їх розвитку та застосування на практиці.
Відзначимо принагідно, що інтерес до вивчення середніх величин виявило чимало зовсім не середніх вчених - від Піфагора та Аристотеля до О.Л. Коші та А.М. Колмогорова.
Початок застосуванню середніх величин в кількісному аналізі суспільних явищ покладено видатним бельгійським вченим ХІХ ст. Адольфом Кетле.
Частина 1. Між двома вогнями
Богам, що живуть на Олімпі,
Середина є до вподоби.
Середня арифметична - улюблениця мільйонів
Вперше про «середні» ми дізнаємося в дитинстві. Середина ріки, середа (середина тижня - якщо рахувати по-біблійному, від неділі до суботи) і т. ін. У всіх цих випадках інтуїтивно під серединою розуміється точка в просторі або в часі, рівновіддалена від двох інших точок, що представляють початок і кінець чого-небудь. Що є математичною моделлю такого роду середніх величин? Їх інтуїтивному введенню відповідають постановка і рішення наступної математичної задачі. Є пара чисел а і b (b > а). Потрібно знайти третє число с, «рівновіддалене» від а і b, тобто таке, що с - а = b - с. Історики науки стверджують, що саме так вводиться поняття середньої величини в працях великого давньогрецького вченого Аристотеля (ІV ст. до н.е.). Ясно, що рішенням цієї задачі є
ca = (a + b)/2.
Це - знайома зі шкільного курсу математики середня арифметична двох чисел а і b. Правда, в школі ця величина вводиться формально, «за визначенням» «середньою арифметичною двох чисел називається півсума цих чисел» - без роз’яснення «фізичної суті».
Середня арифметична і з понятійної, і з математичної точок зору є настільки природною, що у школяра створюється враження, ніби іншого уявлення про середню величину і бути не може. І що «арифметична» - непотрібний словесний додаток.
Улюблена середня Галілея
Перший удар по, здавалося б, «єдиній і неповторній» середній арифметичній наносить геометрія.
Висота h прямокутного трикутника, опущена з вершини прямого кута, більше меншого (ha) й менше більшого (hb) з відрізків, на які ділить гіпотенузу основа цієї висоти.
Формула для обчислення висоти має вигляд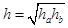 
. «З враженням» від цієї формули величина 
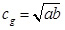названа середньою геометричною чисел а і b (на відміну від середньої арифметичної, середня геометрична вводиться лиш для додатних чисел).
Виявляється, що середня геометрична має й негеометричну інтерпретацію. Якщо (як показано в попередньому пункті) середня арифметична забезпечує рівність відхилень, то до середньої геометричної веде рівність відношень.
Поставимо за мету знайти число сg, що відноситься до а (меншого з двох чисел) так само, як b (більше число) відноситься до cg. Відповідне рівняння (відносно сg) має вигляд: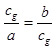 
. Його розв’язком і є середня геометрична чисел а і b.
Яка ж з двох згаданих середніх «більш середня» - арифметична чи геометрична? Іншими словами, яку з них слід використовувати на практиці? Це залежить від цілей, для яких використовується середня. У більшості практичних випадків більш придатною є перша модель, а значить, середня арифметична є «більш середньою». Але не завжди! У 1627 році мала місце документально зафіксована суперечка між самим Галілеєм і якимсь ченцем Ноццоліно. Предмет суперечки полягав в наступному: «якщо коня оцінено двома оцінювачами в 10 і 1000 одиниць, то якій середній слід віддати перевагу в якості величини, що представляє його дійсну ціну? Середній арифметичній, як вважав Ноццоліно, чи середній геометричній, яку вважав за кращу Галілей?» [3]. Значно пізніше (в ХІХ столітті) видатний німецький математик і астроном Філіп Людвіг фон Зейдель (1821-1896), вирішив цю суперечку, довівши на підставі так званого психофізичного закону Вебєра-Фехнера, що «в разі, якщо оцінка ґрунтується виключно на наших сприйняттях, правильно застосовувати середню геометричну, а не середню арифметичну» [3]. Тобто Галілей і тут не помилився!
В пошуках гармонії
Про існування ще двох видів середніх - середньої квадратичної та середньої гармонічної - школярі дізнаються, коли займаються розв’язанням тих самих задач на доведення нерівностей. Ці середні вводяться до розгляду формально.
Перша з них обчислюється за формулою
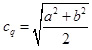
й активно застосовується в загальній [4] і математичній [5] статистиці. А ось друга з них має ряд цікавих змістовних інтерпретацій, одну з яких подано нижче.
За визначенням, середньою гармонічною двох чисел а і 19, таких, що a≠0, b≠0, і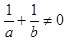 
, називається третє число ch, яке обчислюється за формулою: 
.
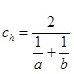Для отримання однієї з можливих інтерпретацій середньої гармонічної розглянемо задачу на визначення середньої швидкості руху автомобіля від пункту А до пункту В і назад, якщо шлях від пункту А до пункту В він їхав зі швидкістю v1 а назад від В до А - зі швидкістю v2. Пригадуємо з початкового курсу фізики, що середня швидкість - це весь шлях, поділений на весь час шляху Позначимо відстань між пунктами через ѕ. Тоді середня швидкість обчислюється за формулою
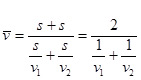
Так от, що таке середня швидкість - це і є середня гармонічна швидкостей руху «туди» і «назад».
Генератор середніх величин
Цікаво, що всі згадані середні виявляються «одного поля ягодами»! Для додатних чисел a і b введемо в розгляд поняття середньої ѕ-го порядку (середньозваженої ѕ-го ступеня):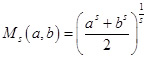 
. Ясно, що M1(a,b) - середня арифметична чисел a і b, M2(a,b) - середня квадратична, M-1(a,b) - середня гармонічна. Але найцікавіше те, що M0(a,b) - це середня геометрична чисел a і b! Правда, тут мається на увазі застосування операції граничного переходу, тобто
.
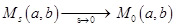«Голими руками» цю границю «не взяти», тому що має місце невизначеність виду 1∞. Але вона легко перетворюється в невизначеність виду 0/0, яка усувається за допомогою всемогутнього правила Лопіталя. Тільки для «крутих», тобто студентів-першокурсників! Робиться це наступним чином: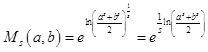 
. Але 
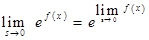, а значить
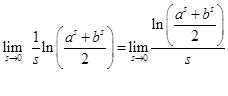
А це вже невизначеність типу 0/0, в цьому разі «викочуємо» правило Лопіталя [6]. Остання границя дорівнює відношенню границь похідних, тобто
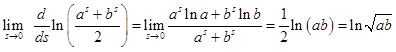
Таким чином,
.
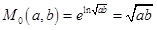Між тим з’ясовується, що параметр ѕ вибудовує середні в певному порядку. Має місце відома лема Йєнсена, а саме: Мѕ як функція від ѕ за умови a=b є сталою, а якщо a ≠b, суворо монотонно зростає, тобто, якщо s1<s2
Ms1(a,b)=Ms2(a,b)=a, Ms1(a,b)<Ms2(a,b) при a≠b.
Доведення цієї леми відносно нескладне. Бажаючі з ним ознайомитись можуть звернутись, наприклад, до [5]. З леми Йєнсена безпосередньо випливає справедливість популярних нерівностей між середньою арифметичною, геометричною, квадратичною тощо [1,2].
(далі буде)
Література:
1. И. Х. Сивашинский. Неравенства в задачах. — М.: «Наука», 1967. — 302 с.
2. И. С. Слонимский. Элементарная алгебра. Дополнительный курс. — М.: «Наука». — 1964. — с.133-136.
3. К. Джини. Средние величины. — М.: «Статистика» — 1970. — 448 c.
4. И. С. Пасхавер. Средние величины в статистике. — М.: «Статистика».– 1979. — 279 с.
5. Г. Кимбл. Как правильно пользоваться статистикой. — М.: «Финансы и статистика». — 1982. — 294 с.
6. Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — с. 130-131.
7. К. Лейхтвейс. Выпуклые множества. — М.: «Наука». — 1985. — с. 250-251.
Б.Г. Тучинський, середній математик, до речі доктор філософії (PhD) за спеціальністю «прикладна математика для економіки», ст. наук. співробітник Інституту відновлюваної енергетики НАН України
Засновник та видавець