За останні дві тисячі років людство зробило величезний порух вперед у всіх життєвих галузях: у будівництві, технологіях, медицині. Рушійною силою цього прогресу завжди була наука. За це честь і хвала вченим всіх часів і народів. Людство зобов’язане їм сучасними досягненнями. Але було б несправедливо не згадати, що цей тернистий шлях до сьогодення людина пройшла не самотужки. Завжди були попутники…

Брати наші менші, тварини, з прадавніх часів повсякчас йшли поруч з людиною і були вірними помічниками і мисливцю, і хліборобу, і воїну, і… вченому. Повчальним є той факт, що багатьом великим відкриттям у сфері біології, медицини людство зобов’язане в першу чергу тваринам. Тваринам, які були відданими асистентами дослідників, які інколи були змушені прийняти мученицьку смерть заради встановлення істини.

Серед них безіменні мавпи, кролики, коти, жаби, щури, миші. Та найвідомішою «науковою співробітницею», мабуть, є знаменита собака Павлова. У своїх дослідженнях російський академік, фізіолог, психолог, творець учення про вищу нервову діяльність, лауреат Нобелівської премії (1904 р.) в області медицини та фізіології  Іван Петрович Павлов (1849-1936) використовував собак. Саме цим істотам корифей фізіології завдячував своїми науковими досягненнями. У 1935 році на території інституту експериментальної медицини в Ленінграді був урочисто відкритий пам’ятник собаці, створений за ініціативою І.П. Павлова на знак вдячності за безкорисне і віддане служіння науці. Цей пам’ятник-фонтан виконаний у вигляді фігури собаки на постаменті, прикрашеному зображеннями голів собак різних порід та барельєфами, що відтворюють картини лабораторного життя. Він набув широкої популярності не лише в Росії, а й в усьому світі.

Іншими відомими «страждальцями науки» стали жаби. Пам’ятників жабам, зрозуміло, набагато менше, ніж собакам. Це пояснюється, мабуть, тим, що ці земноводні не такі симпатичні, як «рябки» і «тузики», але їхній внесок у науку важко переоцінити. Ще в ХІХ сторіччі біля будівлі Пастерівського інституту в Парижі було встановлено пам’ятник жабі. Напис на ньому говорить: «За участь у великому відкритті доктора Гальвані». Нагадаємо, що початком електрофізіології стали багаторічні кропіткі дослідження італійського лікаря Луїджі Гальвані (італ. Luigі  Galvani, 1737-1798), який вивчав електричні явища у клітинах з використанням нервово-м’язового препарату жаби. Подальші досліди на жабах дали змогу вченим накопичити і розширити знання в області фізіології нервової системи, електрофізіології і електрокардіографії.

У Санкт-Петербурзькому університеті височіє скульптурна композиція, на якій вибиті слова: «…человечество должно быть бесконечно благодарным кошке, подарившей миру множество первостепенных открытий в физиологии». Зрозуміло, персонажем цього пам’ятника стала безіменна мурка. У Парижі перед університетом Сорбонна є подібний пам’ятник, який теж звеличує кішку, котра ціною життя допомагала вченим-фізіологам.

Відомі й інші випадки вшанування «чотирилапих науковців». Так, наприклад, у Білорусії в 2008 році біля Гродненського державного медичного університету було встановлено пам’ятник тваринам за неоціненний вклад у розвиток медичної науки.

Не можна оминути увагою і піддослідних гризунів. 1 березня 2009 року виповнилося 100 років лабораторній миші! Ні, ця миша не прожила сторіччя. Просто вчені Гарвардського університету сто років тому стали широко використовувати маленьких гризунів у великій науці. Цікаво знати, що для експериментів та дослідів щорічно необхідно більше 25 мільйонів мишей.

Коли тварини стають помічниками в біології, в медицині – це зрозуміло. Але не поодинокі приклади, коли за допомогою до тварин звертаються і представники інших наук: філософії, хімії, математики і навіть фізики. Зрозуміло, що ці вчені більш гуманно ставляться до братів наших менших, бо використовують не живих тварин, а уявних. Вживання образів тварини дуже часто допомагає глибше розкрити суть проблеми, краще проілюструвати розв’язок задачі, яскравіше сформулювати доведення. Звертання до «звіриних мотивів» дає змогу зрозуміти незрозуміле, запам’ятати те, що важко запам’ятовується. Пригадаємо лише відоме шкільне правило: «Биссектриса – это такая крыса, которая бегает по углам и делит угол пополам». Але це один із найпростіших випадків.

У філософії образи живих істот допомагають виразно розкрити глибинні аспекти явищ. Відому проблему вибору яскраво ілюструє філософський парадокс, названий по імені Жана Буридана (фр. Jean Buridan, 1300-1358). Згідно цього парадоксу, якщо віслюка поставити поміж двох однаково доступних і гарних копиць запашного сіна, то бідна тварина неодмінно помре з голоду допоки буде приймати виважене і обґрунтоване рішення. Ця версія парадоксу набула широкого розголосу завдяки Ляйбніцу і отримала назву – «парадокс Буриданового віслюка». У подальшому вислів «Буриданів віслюк» став фразеологізмом. Ним характеризують людину, що перебуває у крайній нерішучості та не знає яке рішення прийняти.

Нерідко зоологічні порівняння використовували і хіміки. Цікава історія відкриття і дослідження бензолу. Довгий час учені не могли зрозуміти внутрішньої будови цієї речовини. І ось німецький хімік-органік Кекуле (нім. Friedrich August Kekulé von Stradonitz, 1829-1896) одного разу побачив сон. «Довгі ланцюги атомів часто тісно сплетені, безперервно рухалися, звиваючись і розвиваючись, наче змії. Але що ж це? Одна зі змій ухопила себе за хвіст і закружляла перед моїми очима, ніби дражнячи…», – переповідав пізніше своє сновидіння Фрідріх Кекуле. Так учений здогадався про циклічну будову молекули бензолу. З огляду на це, структурну формулу першого представника ароматичного ряду вуглеводнів довгий час називали не інакше як змія Кекуле.

У хімічному серпентарії є й інші змії. Найвідоміші з них – «фараонові змії». Свого часу німецький хімік Фрідріх Вьолер (нім. Friedrich Wöhler, 1800-1882) відкрив і вивчив реакцію розкладу тіоціанату ртуті Hg(NCS)₂. Під час піролізу цієї речовини спостерігалося дивовижне явище, коли з невеличкої кількості вихідного реагенту «виповзала» довга об’ємиста «змія», котра складалася з продуктів розщеплення. За схожість з біблійською легендою, в якій Мойсей налякав фараона змією, що виповзла з його жезла, видовищну реакцію хіміки назвали «фараоновими зміями».

На відміну від хіміків, романтично налаштовані математики використовували у своїх роботах більш миролюбних і красивих істот. У планіметрії, наприклад, існує теорема про метелика, її автор англійський математик Вільям Горнер (англ. William George Horner, 1786-1837). Суть її пояснює деякі властивості хорд, що перетинають одна одну. Але геометрична ілюстрація твердження, яка дуже схожа на метелика, змусила Горнера назвати своє відкриття не теоремою про хорди, а теоремою про метелика.

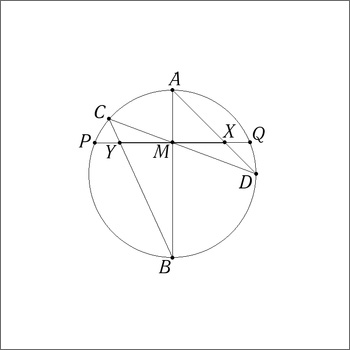
У XVII сторіччі французький математик Етьєн Паскаль (Еtienne Pascal, 1588 – 1651), батько Блеза Паскаля, відкрив і дослідив невідому раніше алгебраїчну криву. Описується вона в прямокутних координатах рівнянням: (x²+y²-ay)²=l²(x²+y²), а в полярних координатах відповідно: ρ=l-asinφ, де a— діаметр вихідного кола, а l — відстань, на яку переміщується точка вздовж радіус-вектора.

Це була лімакона – плоска алгебраїчна крива 4-го порядку; подера кола, конхоїда кола відносно точки на колі, окремий випадок Декартового овалу, вона також являється епітрохоїдою. За свою зовнішню схожість з черевоногими молюсками геометрична крива отримала назву «равлик Паскаля».

Подерою заданої кривої стосовно якої-небудь точки О площини називається нова крива, що являється геометричним місцем точок, які є основами перпендикулярів, опущених з точки О на дотичні до заданої кривої.

Конхоїда кривої — це плоска крива, що виходить при збільшенні або зменшенні радіус-вектора кожної точки даної плоскої кривої на постійну величину.

Декартовий овал – це плоска крива, яка визначається як множина точок М, відстані r₁ і r₂ від якої до двох заданих точок F₁ і F₂,(що називаються фокусами) задовольняє лінійне однорідне рівняння. r₁+mr₂=a, де m і а – сталі числа. При m=1 Декартовий овал перетворюється в еліпс, а при m=-1 – у гіперболу.

Епітрохоїда — це плоска крива, що утворюється точкою, яка жорстко зв'язана з колом, що котиться по зовнішній стороні іншого кола.

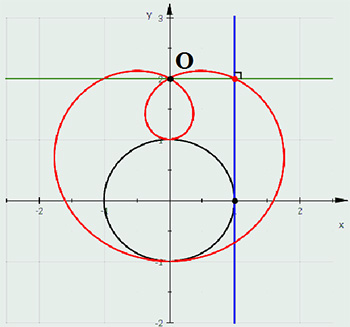
Равлик Паскаля широко застосовується в техніці. Зокрема, при конструюванні ексцентриків, які використовують для перетворення обертового руху у прямолінійний зворотно-поступальний рух; кулачків машин; трібків та зубчатих коліс. Ця геометрична крива також нерідко вживана в оптичній техніці. Термін равлик Паскаля був запропонований французьким математиком Робервалем, сучасником і другом Етьєна Паскаля.

Світ не стоїть на місці, наука рухається вперед, математики у своїх творчих пошуках теж рухаються від простого до складного, від простіших організмів до більш розвинутих. Знайшлось місце в математиці і нашим «предкам» – приматам. Так у теорії ймовірності розглядається теорема про нескінчену мавпу. Ця теорема стверджує, що серед абстрактних мавп, що випадковим чином натискають клавіші друкарських машинок завжди знайдеться одна, що надрукує заданий текст. Мавпа може бути і одна, якщо вона буде займатись цим достатньо довго, то рано чи пізно в неї це вийде. Коли час необмежений і прямує до безкінечності, ймовірність події збільшується. Тобто протягом необмежено довгого проміжку часу така подія неодмінно відбудеться (за умови, що мавпа не помре від старості чи голоду, а друкарська машинка не зламається).

Теорема в науково-популярному вигляді змальовує деякі аспекти теорії ймовірності. Наукового значення вона майже не має, а її популярність у масах пояснюється вдаваною парадоксальністю.

Інший цікавий логічний парадокс сформулював німецький і американський філософ Карл Гемпель (Carl Gustav Hempel, 1905-1997) це парадокс ворон, відомий також як парадокс Гемпеля. Сутність цього парадоксу ілюструє протиріччя між індуктивною логікою та інтуїцією.

Припустимо, говорив Гемпель, що всі ворони чорні. Згідно з формальною логікою це твердження еквівалентно тому, що «не чорні предмети не є воронами». Але цей висновок суперечить інтуїтивному сприйняттю ситуації людиною. Парадокс вирішується за допомогою теореми Байєса.

Не стояли осторонь «співпраці» з тваринами і фізики. І серед цих тварин знову ж таки метелики, коти, коні, їжаки і навіть… демони. Та про все докладніше.

У 1963 році американський математик та метеоролог Едвард Лоренц (англ. Edward Norton Lorenz, 1917 - 2008) записав математичну модель погоди, що складалась із трьох диференціальних рівнянь. Проста система рівнянь демонструвала складну поведінку природних явищ. Математична модель виявила велику чутливість до незначних змін початкових умов. Це наштовхнуло Лоренца на думку про те, що навіть невелика похибка у визначенні початкового стану системи (що неминуче для будь-якої природної системи), унеможливлює прогноз її стану в майбутньому. У подальшому це явище отримало назву ефект метелика. Він є наслідком нестійкості поведінки певних нелінійних дисипативних систем, коли невелика флуктуація початкових умов спричиняє не прогнозовані наслідки. Термін ефект метелика у природничих науках позначає властивість деяких хаотичних систем генерувати непередбачувані ефекти де-небудь у іншому місці і в інший час.

Дивовижним чином пов’язана з метеорологією й інша «тваринна» теорема. Це так звана теорема про причісування їжака. Теорема стверджує, що не існує неперервного дотичного векторного поля на сфері, котре ніде не перетворюється в нуль. Звичайною мовою: неможливо причесати їжака, який має форму сфери так, щоб його голки ніде не настовбурчувалися одна проти одної. Теорема є простим наслідком із теореми про нерухому точку Брауера, доведену в 1912 році.

Цікавим видається застосування теореми в метеорології. Якщо розглядати вітер, як неперервне векторне поле на поверхні планети, то згідно «теореми про їжака» стає зрозумілим механізм утворення циклонів. Адже обов’язково повинна існувати принаймні одна точка на земній кулі, швидкість вітру в якій дорівнює нулю. Ця точка і стане центром циклону чи антициклону. Вітер подібно голкам їжака буде закручуватись навколо цієї точки. Таким чином по теоремі про причісування їжака – якщо десь на Землі дме хоча б який-небудь вітер, то десь обов’язково повинен бути циклон. Виявляється, всі прогнози погоди побічно завдячують своїм існуванням… їжакові та теоремі про його причісування.

Не обійшлось у фізиці і без пухнастих домашніх улюбленців – котів. Для того, щоб проілюструвати неповноту квантової механіки при переході від субатомних систем до макроскопічних австрійський фізик-теоретик, один із засновників квантової механіки, лауреат Нобелівської премії з фізики (1933 р.) Ервін Шрьодінгер (нім. Erwin Rudolf Josef Alexander Schrödinger, 1887-1961) запропонував уявний експеримент, героєм якого став його знаменитий кіт – так званий кіт Шрьодінгера.

Уявного кота фізик «посадив» у коробку, перебуваючи в котрій кіт з імовірністю 1/2 міг бути живим, або з такою ж імовірністю – мертвим. Згідно з принципами квантової механіки, кожна елементарна частинка одночасно може перебувати в кількох станах. Аналогічно й кіт Шрьодінгера за умовами експерименту міг бути водночас живим і мертвим, доти, доки хтось не відчинить коробку й не визначить його реальний стан. Чи живий кіт, чи ні?

Оскільки ясно, що кіт обов'язково мусить бути або живим, або мертвим (не існує стану, проміжного між життям та смертю), то це справедливо і для атомного ядра. Воно мусить бути або таким, що розпалося, або таким, що не розпалося!

Так на долю звичайного кота випало вирішувати майбутнє квантової фізики. З часом кіт Шрьодінгера став свого роду зіркою. Цей персонаж частенько з’являється на сторінках книг, в серіалах та художніх фільмах. Зауважимо, що кіт Шрьодінгера насправді був не котом, а… кішкою, про це свідчать першоджерела.

Популярність котів у науці безперечно обумовлена великою любов’ю вчених до цих чотирилапих друзів. Це породжує дивні відкриття на кшталт парадокса кішки з маслом.

Парадокс кішки з маслом – жартівливий псевдопарадокс, що базується на двох народних мудростях: кішка завжди приземлюється на лапи; бутерброд завжди падає маслом вниз. Як закінчиться падіння кішки, якщо до спини їй прикріплено бутерброд, причому маслом догори? Дехто стверджує, що результатом експерименту може стати прояв «антигравітації». За словами «теоретиків», падіння кішки повинно сповільнитися з наближенням до землі. А сама вона почне обертатися, намагаючись приземлитися на лапи, але в той же час і на масло бутерброда. Врешті-решт, вона повинна сягнути стабільного стану, висячи недалеко від поверхні землі та обертаючись із великою швидкістю. Це в свою чергу було б можливим лише за відсутності атмосфери, але, відповідно до закону збереження енергії, опір повітря повинен вичерпати гравітаційну енергію падіння. Також існує думка, що кішка злиже масло з бутерброда та приземлиться на лапи, однак таке припущення безпідставне, тому що кішка не може дістати язиком до середини своєї спини. Серйозність і наукова цінність цього парадоксу не викликає сумнівів – це просто дотепний науковий жарт.

Вчені, як відомо, люди дуже серйозні і, як наслідок, дуже великі жартівники. Їхня винахідливість не має меж. Коли їм не вистачає для дослідів реальних існуючих тварин вони починають вигадувати неіснуючі істоти, фантастичні створіння з неймовірними здібностями. Найвідомішим представником когорти мутантів є так званий «сферичний кінь у вакуумі».

Цим виразом позначають деяку ідеальну концепцію, абсолютно відірвану від реальності. Вираз походить із наукового анекдоту, коли вченим-фізикам запропонували спрогнозувати результат кінних перегонів, вони розробили цілу теорію, що описувала рух абсолютно пружного сферичного коня у вакуумі. Як з’ясувалося згодом, основна задача, яку покликаний виконувати сферичний кінь у вакуумі, носила не фізичний, а більшою мірою етичний характер. Сферичний кінь став інструментом для створення пародій, критики та висміювання занадто ідеалізованих теорій, припущень, моделей на зразок: «абсолютно пружне тіло», «ідеальний газ», «ідеальна сферичність об’єктів». Про самого ж сферичного коня достеменно відомо, що він суперсиметричний кінь, з усіх боків кінь, якби ви на нього не дивились. Іржання сферичного коня є монофонічною гармонікою і розповсюджується без розсіювання навіть у вакуумі. Волосся з хвоста сферичного коня має нескінчену довжину, абсолютно не здатне до розтягування та має товщину і масу, якими можна знехтувати.

Існуванням самого ж сферичного коня знехтувати не можна ніяк. У Берліні навіть встановлено пам’ятник цій дивовижній науковій істоті.

Розмаїття живого світу, що нас оточує, повсякчас осявало і надихало вчених до нових звершень, нових теорій. Та коли бракувало біорізноманітності реального світу, вони створювали істот, яких взагалі ніхто не бачив, ніхто не чув, і в природі не існує.

Шотландський учений Джеймс Максвелл (англ. James Clerk Maxwell, 1831-1879) став загальновідомим завдяки створеній ним теорії електромагнітного поля, дослідженням у галузі електрики, магнетизму і оптики. Крім цього, Максвеллу належать великі відкриття і в інших напрямках фізики, зокрема молекулярної кінетичної теорії газів. Вивчаючи термодинаміку, Максвелл вигадав у 1867 році уявний експеримент, головним героєм якого  була гіпотетична розумна істота мікроскопічного розміру – так званий демон Максвелла.

Демон (грец. δαίμων) — міфологічне створіння, дух із надлюдською силою, що належить до невидимого світу і має вплив на життя й долю людей.

Волею Максвелла цей мудрий демон розташовувався біля отвору, що сполучав дві частини посудини, розділені непроникною перегородкою. За задумом ученого його піддослідний демон мав цікаву властивість – він дозволяв швидким (гарячим) молекулам газу пролітати тільки з лівої частини в праву, а повільним (холодним) навпаки – тільки з правої в ліву. Тоді через певний проміжок часу всі гарячі молекули мають сконцентруватися в одній частині посудини, а холодні – в іншій. Таким чином фантастичний демон Максвелла нібито дає змогу нагріти одну частину системи і охолодити іншу без залучення додаткової зовнішньої енергії, що суперечить термодинамічному принципу, згідно якого ентропія замкнутих систем не зменшується. Цей експеримент мав на меті проілюструвати псевдопарадоксальність Другого начала термодинаміки. Парадокс вирішується, якщо взяти до уваги те, що для існування самого демона теж необхідна енергія від зовнішнього джерела. Дивовижно, але уявний експеримент Максвелла в реальності вдалося відтворити у 2010 році фізикам із університетів Тюо (Chuo University) і Токіо (University of Tokyo). Лабораторна установка, що містила в собі дві полістиролові кульки діаметром 0,3 мікрометра (одна з яких оберталася навколо іншої) була заповнена рідиною. Молекули рідини завдяки броунівському руху підштовхували рухому кульку-ротор, зрозуміло, з однаковою ймовірністю як за годинниковою, так і проти годинникової стрілки. Але далі експериментатори додали до системи «демона» – надшвидкісну камеру, що спостерігала за кулькою і комп’ютер, який керував електричним полем. Цим забезпечувався зворотний зв'язок. Коли ротор обертався у заданому напрямку, система не вмішувалась в його рух, якщо ж ротор намагався повернутися у зворотний бік, зовнішнє електричне поле блокувало його. Так був створений аналог дверцят, котрі відчиняє і зачиняє демон Максвелла. При чому ротор збільшував свою енергію виключно за рахунок теплового руху молекул. Зауважимо, що установка ні в якому разі не порушує законів природи, адже для існування «демона», що включає камеру, комп’ютер, систему корекції, необхідна зовнішня енергія. Цікаво, що термін «демон» запропонував Вільям Томсон, лорд Кельвін, тоді як сам Максвелл більше схилявся до назви «клапан».

Звернення до образу демона було доволі популярним в ті часи. Так П'єр-Сімон Лаплас (фр. Pierre-Simon Laplace, 1749-1827) – французький математик і астроном; відомий своїми працями в області диференційних рівнянь, один із творців теорії ймовірностей ще у 1814 році використав персонаж демона в уявному експерименті. У ньому ця вигадана, розумна істота (гіпотетичний вищий розум), сприйнявши інформацію про розташування і швидкість будь-якої точки у Всесвіті, здатна була відтворювати еволюцію цієї точки як в майбутньому, так і в минулому. Придумано цю істоту було для наочної ілюстрації міри нашої необізнаності та необхідності статистичної інтерпретації деяких реальних процесів у навколишньому світі.

Проблематика Демона Лапласа пов’язана здебільшого не з можливістю детерміністичного прогнозування подій на практиці, а з тим, чи можливе воно теоретично взагалі. Деякі джерела стверджують, що опис гіпотетичного розуму як «демона» належить не Лапласу, а його біографам. Лаплас бачив себе перш за все вченим, і вважав, що людство може глибше зрозуміти світ самотужки завдяки розвитку науки.

Це, мабуть, далеко не повний перелік наукових досягнень, славу за які вчені мають розділити з братами нашими меншими. Поза увагою цієї оповіді залишилось багато цікавих фактів, пов’язаних з використанням тварин та тваринних образів в науці. Безперечно, допитливий читач обов’язково поцікавиться і з’ясує для себе, що таке теорія Чорного лебедя, задача про коней одного кольору, проблема курки та яйця, парадокс Ахіллеса і черепахи, мурашиний алгоритм, і нарешті, гіпотеза зоопарку.

Тож чи можна вважати людину єдиним, одноосібним творцем науки? Чого ми варті без наших чотирилапих, пернатих, земноводних, перетинчастокрилих, черевоногих помічників та співавторів у наукових шуканнях?

За матеріалами інтернет-видань.

Л.О. Ревуцька